Inégalité

Soient .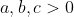


Montrer que :

Spoiler:

Appliquer deux fois IAG donne directment le résultat

D'après IAG : LHS>=(ab/c)+(bc/a)+(ac/b)
IAG encore une fois (ab/c)+(bc/a)+(ac/b) >= a+b+c
D'où la conclusion.

Parfait comme d'habitude Mr. Nayssi.

haha! Merci

on utilise une inégalité très utile .
x²+y²+z²>=xy+yz+xz

Réordonnement quoi!

j'aimerais bien voir une solution complete utilisant l'inégalité du réordonnement , car je ne maîtrise po trop cette inégalité surtout les cas ou on peut ordonner les thermes.

Mais le réordonnement tout seul ne donne pas le résultat. Pour cela, on remarque que l'inégalité est homogène d'ordre 1, donc on peut normaliser en posant a+b+c=1 comme ça le résultat se conclut rapidement.
Maintenant que je le pense Chebychev +AM-GM donne une autre démo aussi.

Attendez pour que je rédige une autre réponse en utilisant Réordonnement + IAG .

Soient .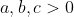

On veut montrer que :








Par symétrie de rôles, on peut supposer que :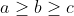

donc

D'après l'inégalité du réordonnement (deux fois) on a :



et

La somme donne :



(D'après IAG)



Et il est facile de vérifier que :

Donc:



D'où:

D'où le résultat voulut.

CQFD.


Et j'attends toujours vos remarques et observations.

Tu aurais pu dès que a^4+b^4+c^4 >= abc (a+b+c) utiliser le réordonnement autrement sans passer de l'AM-GM.
Par symétrie de roles tjrs a>=b>=c Alors
a^2>=b^2>=c^2 et ab>=ac>=bc alors a^4+b^4+c^4=a^2*a^2+b^2*b^2+c^2*c^2>= a^2bc+ab^2c+abc^2=abc(a+b+c)

n.naoufal a écrit:

Tu aurais pu dès que a^4+b^4+c^4 >= abc (a+b+c) utiliser le réordonnement autrement sans passer de l'AM-GM.
Par symétrie de roles tjrs a>=b>=c Alors
a^2>=b^2>=c^2 et ab>=ac>=bc alors a^4+b^4+c^4=a^2*a^2+b^2*b^2+c^2*c^2>= a^2bc+ab^2c+abc^2=abc(a+b+c)

Si, j'ai pas pensé à ça... Sinon, la méthode qu'a présenté Nayssi au début reste la plus simple et la plus belle ...

L'inégalité étant facile et cyclique il y a beaucoup plus de chance de pouvoir la prouver par plusieurs méthodes

Mr. n.naoufal pourriez vous nous expliquer l'homogénéité, j'ai jeté un coup d'œil sur le cour d'Animaths mais sans résultats, il me paraît bourbeux et un peu avancé pour mon niveau.

j’espère qu'il le ferait

On dit qu'une fonction est homogène de dégrée k si et seulement si f(a*x)=a^k*f(x) pour tout a >0 et w<> du vecteur nul.
Ainsi on peut utiliser à la place de a,b et c dans une inégalité a/||a||,b/||b|| et c/||c||
avec || || une norme quelconque. on peut ainsi utiliser des conditions comme a+b+c=1 ou abc=1 ceux si dépendent encore de la norme choisie.
Mais généralement, pour les élèves de lycée, tu peux parler d'homogénéité sans évoquer une quelconque norme.
Voilà pour t’entraîner sur les techniques d’homogénéité et de normalisation je te conseille le fabuleux livre de Hojoo Lee que tu trouveras ici : http://www.eleves.ens.fr/home/kortchem/olympiades/Cours/Inegalites/tin2006.pdf

Pour avoir un petit aperçu de cette théorie je te conseille ce petit résumé.
http://www.math.rice.edu/~njd2/documents/inequalities.pdf
N.B: les deux document sont en anglais donc j'espère que tu maîtrises un peu la langue Bonne lecture

Citation :

j’espère qu'il le ferait

je suis sensé travailler mes oraux, je ne suis pas tout le temps disponible, peut être après la fin de ceux ci

Merci bien M.naoufal

Je vous en prie.

Soient x,y,z des réels strictement positifs.
M.Q: xyz>=(x+y-z)(x+z-y)(y+z-x)

on procède avec les substitutions suivante :
x+y-z=a x-y+z=b -x+y+z=c
l’inégalité est donc équivalente a
(a+b)(b+c)(a+c)>=8abc
IAG finit la démonstration

Oui c'est exact.

boubou math a écrit:

on procède avec les substitutions suivante :
x+y-z=a x-y+z=b -x+y+z=c
l’inégalité est donc équivalente a
(a+b)(b+c)(a+c)>=8abc
IAG finit la démonstration

BOUBOUUUU
Je crois que t'as utlisé le lemme d'Hychschneifer dans le plan Euclidien.
Mais je pense que ce lemme a des conditons : les vecteurs de l'espace hymévirieux doivent etre Schnedifériés ce qui se traduit dans le plan EUCLIDIEN que a,b,c doivent etre positifs
Est-il le cas dans l'exercice ?

expert-run a écrit:

Oui c'est exact.

quoi?

je t'avais deja conseillé d'aller sur SKYPE pour réviser

je vous présente un indice Pour la bonne solution :
remarquer que x(x-y)(x-z)+y(y-x)(y-z)+z(z-x)(z-y)=xyz-(x+y-z)(x+z-y)(y+z-x)

**

Une autre chose expert-run t'es en en premiere et t'as pas le droit de juger une solution comme correcte dans l'espace TRON COMMU c'est de la honte
je crois qu'on a pas regretté notre décision d'hier celle que le kénitrai sera le seul représentant du Maroc au IMO

Je crois que tu comprends rien toi : Supposons que x>=y>=z
alors a>=0 et b>=0 mais c>=0 ou c<=0 alors si c<=0 c est normal car un positif et plus grand d'un négatif et si c>=0 alors on applique I.A.G
Compris??