Inégalité

boubou math a écrit:

on procède avec les substitutions suivante :
x+y-z=a x-y+z=b -x+y+z=c
l’inégalité est donc équivalente a
(a+b)(b+c)(a+c)>=8abc
IAG finit la démonstration

c'est faux, on peut appliquer IAG à condition que tous les nombres soient positifs... (on ne sait pas si -x+y+z et x+y-z et x-y+z sont positifs)

Puisque l'inégalité est symétrique on peut supposer que donc . cette condition est suffisante pour que x,y,z (ils sont tous positifs ) soient les longueurs des côtés d'un triangle ... le résultat en découle d'aprés la substitution de ravi et IAG.

Ali-mes la réponse de boubou n'est pas fausse .Sauf qu'il a négligé une étape:
Comme ta mentionné;puisque l'inégalité est symétrique on peut supposer que x>=y>=z
alors x+y-z=a>=0 et x-y+z=b >=0 mais -x+y+z=c peut être positif ou négatif .
Comme à dit boubou l'inégalité est donc équivalente a :(a+b)(b+c)(a+c)>=8abc
Alors si c<=0 c est trivial
Et si c>=0 on applique la fameuse I.A.G

Et pour toi Mehdi.A c'est honte que tu corriges les copies des olympiades car t es pas quelqu'un de qualifié.

expert_run a écrit:

Ali-mes la réponse de boubou n'est pas fausse .Sauf qu'il a négligé une étape:
Comme ta mentionné;puisque l'inégalité est symétrique on peut supposer que x>=y>=z
alors x+y-z=a>=0 et x-y+z=b >=0 mais -x+y+z=c peut être positif ou négatif .
Comme à dit boubou l'inégalité est donc équivalente a :(a+b)(b+c)(a+c)>=8abc
Alors si c<=0 c est trivial
Et si c>=0 on applique la fameuse I.A.G

Et pour toi Mehdi.A c'est honte que tu corriges les copies des olympiades car t es pas quelqu'un de qualifié.

Il y a une raison pour laquelle tu t'es appelé expert-RUN pas expert-math alors nod t runné m3a rask jéériiiiii !

***

Tu as pas trouvé quelque chose a dire alors tu dis n'importe quoi pffff tu es quelqu'un de fruste .

expert_run a écrit:

(a+b)(b+c)(a+c)>=8abc
Alors si c<=0 c est trivial (a,b>=0)

Et pour toi Mehdi.A c'est honte que tu corriges les copies des olympiades car t es pas quelqu'un de qualifié.

QUoi ? ayawyaaaaaaaah aabaraka mtadfaaaaaaach sir khdém sur SKYYPE
a ch7al fik dial takhraj l3aynin wa baaaaaaazz
Pren a=12 , b=0.1 , c=-2
**

j'aurai honte à ta place d'écrire cela
tu dis prend a=12 , b=0.1 , c=-2 ce qui implique que x=12,1/2 et y=5 et z=-1,9/2 hh et ce qui est contradictoire avec l'énoncé qui dit que x;y;z sont des réels strictement positifs.

A ta place je dirai goodbye les maths ^^

acé normaal ya bdfach lakhor car l'inégalité initiale est vrai pour tout positifs ce qui donne pas surement le fait que a,b,c>0 et SI c<0 on peut pas montrer que (a+b)(b+c)(a+c)>=8abc car elle est fausse en génral et toi dans ta solution t'as dit que si c=<0 alors c'est trivial car (a+b)(b+c)(a+c)>0 ce qui n'est pas toujours le cas sauf pour des conditions précises j'espère que tu as compris et la prochaine fois fais un raissonnement correct
car l'inégalité initiale c''est pas IAG
Je te répondrai plus dans cette rubrique sauf si tu avou qu t'avais pas raison et si tu l'avoue pas tu aura bcp de problème avec moisss ...
sinon voici mon compte SKYPE : ANTI.EXPER-RUN
**

hmm , je vois que tu n'as pas répondu , c'est normal, je vais t'expliquer encore pour que tu puisse comprendre(là je vais travailler dans un plan euclidien)

expert_run a écrit:

j'aurai honte à ta place d'écrire cela
tu dis prend a=12 , b=0.1 , c=-2 ce qui implique que x=12,1/2 et y=5 et z=-1,9/2 hh et ce qui est contradictoire avec l'énoncé qui dit que x;y;z sont des réels strictement positifs.
A ta place je dirai goodbye les maths ^^

expert_run a écrit:

(a+b)(b+c)(a+c)>=8abc
Alors si c<=0 c est trivial (a,b>=0).

maintenant j'ai compris , nta lettre , je crois sciences humaines(car tu as essayé de m'analyser) wla tu apprends chi 7arfa fchi garage, mon ami y a les mathématiques et y a ce qu'on appelle les matématék !et je crains que c'est ce que tu es en train de faire ici !
je suis en train de juger ton raisonnement , et non pas les données de l'exercice, regarde ce que tu as ecris , tu as dis si c<=0 alors il est trivial de montrer que (a+b)(b+c)(a+c)>=8abc!!!!!!!!!!!!!!!!!! et tu n'as pas parlé des conditions de l'exo !!! tu dis donc que c'est vrai pour tous a,b>=0 et c=<0 ce qui est jugé faux d'après le contre exemple que je viens de donner !
en d'autres mots dans un plan non euclidien , celui de Lobatchevsky , si un sous groupe d'un groupe comutatif symétrique est mené d'une loie astroexpertruninienne , les relations de Knuth assurent l'existence d'un élément régulier dont on doit se débarrasser , sinon les mathématiques seront en danger!!
khali donc 3lék lmaths et concentres toi sur l7arfa li rak tt3llemha flgarage!7ta l7arfa meziana !
*

ali-mes a écrit:

Soient .


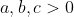Montrer que :

Spoiler:

Par Hölder : .

Mehdi lwaakii :
J'ai donné des Ordres a metaich (oxford University) de ne pas accepter toute solution contenant HOLDER Pour une petite raison

Spoiler:

c'est POur cela j'aime bien IAG qui était l'une de mes collègues dans la classe MP**************
et elle m'a proposé que dans le plan Euclidien on utillise la somme SCHVétérienne en ajoutan 2(a+b+c) à chaque côté
Puis a^3/bc+ b+c> 3bc et la somme héxapyrémlique nous donne le résultat .
**

Medi.A je vais jamais arrivé a te convaincre

ali-mes a écrit:

boubou math a écrit:

on procède avec les substitutions suivante :
x+y-z=a x-y+z=b -x+y+z=c
l’inégalité est donc équivalente a
(a+b)(b+c)(a+c)>=8abc
IAG finit la démonstration

c'est faux, on peut appliquer IAG à condition que tous les nombres soient positifs... (on ne sait pas si -x+y+z et x+y-z et x-y+z sont positifs)

Puisque l'inégalité est symétrique on peut supposer que donc . cette condition est suffisante pour que x,y,z (ils sont tous positifs ) soient les longueurs des côtés d'un triangle ... le résultat en découle d'aprés la substitution de ravi et IAG.

En effet j'ai sauter quelque étape ,je rectifie
si x et y et z ne sont po des coté de triangle alors l'inégalité est vrai car xyz>0 et (x+y-z)(x-y+z)(-x+y+z)=<0
sinon si c'est le contraire
on procède avec les substitutions suivante :
x+y-z=a x-y+z=b -x+y+z=c
l’inégalité est donc équivalente a
(a+b)(b+c)(a+c)>=8abc
IAG finit la démonstration
merci pour la remarque

[quote="boubou math"][quote="ali-mes"]

boubou math a écrit:

(x+y-z)(x-y+z)(-x+y+z)=<0

Pourquoi? C'est incorrect
et arrête de BOUBOUER les voisins doivent dormir ...
**

MEHDI.A degage!! rak khrajti 3la lforum
sir lik ldar l3ajaza ou khalli les jeunes amateurs de maths ikhadmo !!

HamzaBk a écrit:

MEHDI.A degage!! rak khrajti 3la lforum
sir lik ldar l3ajaza ou khalli les jeunes amateurs de maths ikhadmo !!

tatgol l ton grand papi dégage et tu ose t'appeler un amateur de math !
bous yéd jdék w7tarmo wskatna wchuf dakchi li kaigol ra 3ando sé7
galik amateur de math pchaaa5
***

salut tt le monde je vx travailler des exercices de maths d'olympiades mais je n'ai pas trouver des exercices donc si vous connaisez des sites , il sera gentil de me les donner
(je cherche des exercices d'olympiades de 1 ere bac science maths )
merci d'avance

Salut,et si vous proposez des exercices ca serait mieux que de vous chamailler, Au travail!!!!!!

d'accrd merci c'est trés gentil voici un exercice

...??
Enfin, rien ne s'affiche!

a , b et c sont des réels strictement positifs.

Montrer que



a^2/(a+ b)(a +c) +b^2/(b +a)(b +c)+ c^2/(c+ a)(c +b) >= 3/4

hind nassri a écrit:

a , b et c sont des réels strictement positifs.

Montrer que



a^2/(a+ b)(a +c) +b^2/(b +a)(b +c)+ c^2/(c+ a)(c +b) >= 3/4

aprés simplification (taw7id ma9am ...) on a : ce qui vrai par AM-GM (aplication direct) . avec l'egalité si et seulement si a = b = c .

ali-mes a écrit:

Soient .


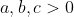Montrer que :

Spoiler:

supposons que : a>=b>=c
alors par inégalité de réordonnement on a : .
et d'aprés C.S on a :
C..Q.F.E