| | série d'éxos logique |  |
|
|
| Auteur | Message |
|---|
sanfoura9
Féru
 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
| | Sujet: série d'éxos logique Jeu 21 Juil 2011, 10:12 | |
| http://arabmaths.kegtux.org/maths09/lycee/1sm/slogique1sm.pdf J'ai fais l'exo 8 mais je doute encore , svp partagez vos réponses  | |
|
| | |
ali-mes
Expert sup
 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: série d'éxos logique Jeu 21 Juil 2011, 20:11 | |
| J'ai bien aimé cette série, mais la plupart des exos sont triviaux. Je vais commencer par résoudre les 2 premiers exos, et peut-être je vais terminer après. Donc, sans perte de temps, je vous propose mes réponses: Exercice 1:- Spoiler:
Exercice 2:- Spoiler:
Soient a,b et c les longueurs des côtés d'un triangle vérifiant a+b+c=1. On a d'après l'inégalitè triangulaire: 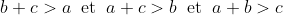 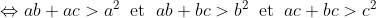 . %3E%20a^2+b^2+c^2) +(a^2+b^2+c^2)%3E2(a^2+b^2+c^2)) ^2%3E%202(a^2+b^2+c^2)\Leftrightarrow%202(a^2+b^2+c^2)%3C%201) 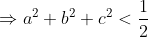 . Donc: 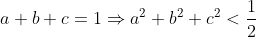 En effet, c'est quoi مثلث محترم ? LMFAO
| |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: série d'éxos logique Jeu 21 Juil 2011, 20:47 | |
| Je continue avec l'exercice 3: Exercice 3:- Spoiler:
| |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: série d'éxos logique Jeu 21 Juil 2011, 21:26 | |
| Exercice 4:- Spoiler:
Soient x et y deux réels: On a: (y+\sqrt{y^2+1})=1\Leftrightarrow%20x+y=0%20\right%20)\;%20\Leftrightarrow) (y+\sqrt{y^2+1})=1\Rightarrow%20x+y=0%20\right%20)\;%20\;%20\textrm{et}\;%20\;%20\left%20(%20x+y=0\Rightarrow%20(x+\sqrt{x^2+1})(y+\sqrt{y^2+1})=1\right%20)) Montrons d'abord: (y+\sqrt{y^2+1})=1\Rightarrow%20x+y=0%20\right) On suppose que: (y+\sqrt{y^2+1})=1) Et on montre que: 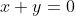 . (y+\sqrt{y^2+1})=1\Rightarrow%20x+\sqrt{x^2+1}=\frac{1}{y+\sqrt{y^2+1}}\;%20\;%20\textrm{et}\;%20\;%20y+\sqrt{y^2+1}=\frac{1}{x+\sqrt{x^2+1}}) (y-\sqrt{y^2+1})}\;%20\;%20\textrm{et}\;%20\;%20y+\sqrt{y^2+1}=\frac{x-\sqrt{x^2+1}}{(x+\sqrt{x^2+1})(x-\sqrt{x^2+1})}) ^2}\;%20\;%20\textrm{et}\;%20\;%20y+\sqrt{y^2+1}=\frac{x-\sqrt{x^2+1}}{x^2-(\sqrt{x^2+1})^2}) }\;%20\;%20\textrm{et}\;%20\;%20y+\sqrt{y^2+1}=\frac{x-\sqrt{x^2+1}}{x^2-(x^2+1)}) 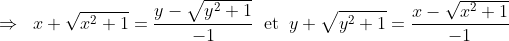 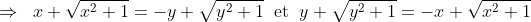 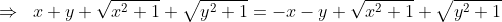 \Leftrightarrow%202(x+y)=0\Rightarrow%20x+y=0) Donc: (1) Maintenant, montrons que: (y+\sqrt{y^2+1})=1) On suppose que: 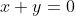et on montre que: . On a 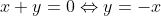 . Et on a: (y+\sqrt{y^2+1})=(x+\sqrt{x^2+1})(-x+\sqrt{x^2+1})) (y+\sqrt{y^2+1})=(\sqrt{x^2+1})^2-x^2=x^2+1-x^2=1) Donc: (2) D'après (1) et (2) on a: (y+\sqrt{y^2+1})=1\Leftrightarrow%20x+y=0%20\right%20)\;%20)
Dernière édition par ali-mes le Ven 22 Juil 2011, 00:57, édité 1 fois | |
|
| | |
az360
Expert grade2
Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
| | Sujet: Re: série d'éxos logique Jeu 21 Juil 2011, 23:52 | |
| Exercice 4: On a : (y%20+%20\sqrt{y^{2}%20+%201})=1%20\Leftrightarrow%20-(y%20+%20\sqrt{y^{2}%20+%201})%20=%20x%20-%20\sqrt{x^{2}%20+%201}) La mémé façon avec y . et avec la somme des deux on de déduit que : x + y = 0 | |
|
| | |
sanfoura9
Féru
Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
| | Sujet: Re: série d'éxos logique Ven 22 Juil 2011, 13:42 | |
| - ali-mes a écrit:
- Je continue avec l'exercice 3:
Exercice 3:
- Spoiler:
méthode plus facile : on a : a>3 ET b>3 et c>3 donc : ab>3b et bc>3c et ac>3a d'où : ab +bc+ac > 3 (a+b+c) 2/ on a : abc> 3bc et abc >3ac et abc >3ab d'où : 3abc > 3( ab + bc +ac) Alors : abc> ab+bc+ac | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: série d'éxos logique Ven 22 Juil 2011, 15:59 | |
| Comme promis, je continue avec les autres exos: Exercice 5:- Spoiler:
| |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: série d'éxos logique Ven 22 Juil 2011, 19:35 | |
| Exercice 6:- Spoiler:
Considérons les assertions suivantes: 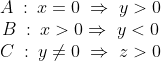 supposons que x=0, donc d'après (A) on a: 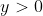 d'où: 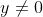 . Donc d'après (C) on a: 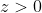 . Donc: ) Ce qui est contradictoire avec le fait que l'un des trois nombres est strictement négatif. On conclut que: 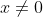 Donc: 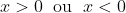 . Si 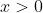 , donc d'après (B) on a: 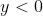 donc 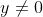. Donc d'après (C), on a: 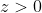. D'où: ) Ce qui est contradictoire avec le fait que l'un des nombres est nul. Cela implique que x est strictement négatif, donc l'un des nombres y ou z est nul et l'autre est strictement positif. Supposons que: 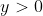donc 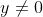. D'après (C) on a: 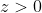. Ce qui est contradictoire avec le fait que l'un des nombres y ou z doit être nul. Le seul cas qui reste est: x est strictement négatif, y est nul et z est strictement positif.
Exercice 7:- Spoiler:
Soient a et b deux réels strictement positifs vérifiant a+b=1, et soit n un entier naturel. On a: (1+\frac{1}{b^n})=1+\frac{1}{b^n}+\frac{1}{a^n}+\frac{1}{a^nb^n}) . Et on a: ^2\geq%200) 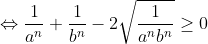 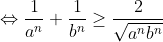 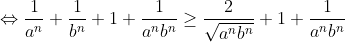 (1+\frac{1}{b^n})\geq%20\frac{2}{\sqrt{a^nb^n}}+1+\frac{1}{a^nb^n}) (*) Et on a: ^2\geq%200) 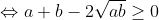 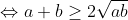 ^2\geq%204ab) 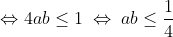 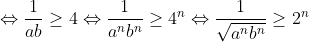 On a donc: ^2+2\times%202^n\times%201+1=(2^n+1)^2) (**). De (*) et (**) on conclut que: (1+\frac{1}{b^n})\geq%20(1+2^n)^2) .
| |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: série d'éxos logique Dim 24 Juil 2011, 15:58 | |
| Exercice 8:- Spoiler:
Il faut ajouter la condition que c est strictement positif, sinon on peut facilement trouver un contre exemple. Comme d'habitude, soient a et b deux réels et soit c un réel strictement positif. 1)- Pour la partie: ( 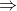 ): On suppose que: ) et on montre que: 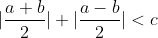 . Donc Il suffit de montrer que: ^2%3C%20c^2) ^2+(\frac{a-b}{2})^2+2|\frac{(a+b)(a-b)}{4}|%3C%20c^2) 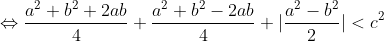 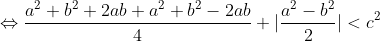 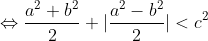 * Si: 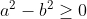 . Donc on aura: 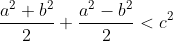 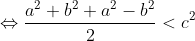 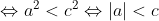 Ce qui est est vrai d'après notre hypothèse. * Si: 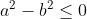 . Donc on aura: 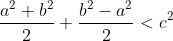 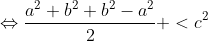 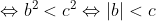 . ce qui est vrai d'après notre hypothèse. Dans les deux cas, on a: \Rightarrow%20|\frac{a+b}{2}|+|\frac{a-b}{2}|%3C%20c) . 2)- Pour la partie: ( 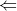 ): On suppose que: 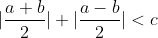et on montre que: . On va utiliser cette propriété: \in%20\mathbb{R}^2):\;%20|x+y|\leq%20|x|+|y|) . On a: 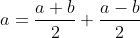 . Donc: 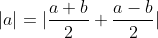 . Donc: 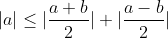 . Et on a: 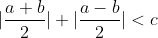Donc: 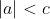 . Et on a: 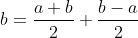 Donc: 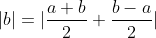 Donc: 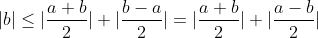 Et on a: 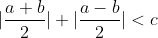Donc: 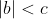 . On conclut que: ) . Synthèse: ) .
| |
|
| | |
wentworth
Féru
Nombre de messages : 55
Age : 28
Date d'inscription : 04/09/2011
| | Sujet: Re: série d'éxos logique Jeu 06 Oct 2011, 23:49 | |
| x et y appartient a R+ et x+y=1
n appartient a N
montrer que
(1+1/x^n)(1+1/y^n)>=( 1+2^n)² | |
|
| | |
*youness*
Maître
Nombre de messages : 132
Date d'inscription : 16/08/2011
| | Sujet: Re: série d'éxos logique Jeu 06 Oct 2011, 23:58 | |
| regarde spoiler d'exercice 7 !!!! | |
|
| | |
diablo902
Maître
Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
| | Sujet: Re: série d'éxos logique Ven 07 Oct 2011, 13:51 | |
| Mais ce n'est pas du tronc commun | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: série d'éxos logique | |
| |
|
| | |
| | série d'éxos logique | |
|
