| | Pour en etre sur ! |  |
|
|
| Auteur | Message |
|---|
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Pour en etre sur ! Sujet: Pour en etre sur !  Dim 21 Aoû 2011, 14:56 Dim 21 Aoû 2011, 14:56 | |
| deux petites questions , 1) 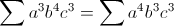 ?? puisqu'il ne joue qu'un role cyclique si on developpe le tout , on aura la meme cigma cyclique , je me demande si c vrai, la meme chose pour celle ci : 2) 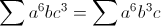 ??? | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Dim 21 Aoû 2011, 15:25 Dim 21 Aoû 2011, 15:25 | |
| oui je crois c'est la meme chose ...
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Dim 21 Aoû 2011, 16:13 Dim 21 Aoû 2011, 16:13 | |
| Je profite de ce topic pour poser ces deux questions: Quelle différence existe entre:  et  ? A-t-on: =a+b+c) ? Merci d'avance pour les réponses. | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Dim 21 Aoû 2011, 16:20 Dim 21 Aoû 2011, 16:20 | |
| @nmo , qu'en pense tu ? est ce que ce que j'ai dis est juste ou faux ? | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Dim 21 Aoû 2011, 16:46 Dim 21 Aoû 2011, 16:46 | |
| - nmo a écrit:
- Je profite de ce topic pour poser ces deux questions:
Quelle différence existe entre:  et et  ? ?
A-t-on: =a+b+c) ? ?
Merci d'avance pour les réponses. je te réponde nmo voila : "Cyclique": %20=%20f(x,y,z)%20+%20f(y,z,x)%20+%20f(z,x,y)) Exemple :  "Sum" "Sum" : %20=%20f(x,y,z)%20+%20f(x,z,y)%20+%20f(y,x,z)%20+%20f(y,z,x)%20+%20f(z,x,y)%20+%20f(z,y,x)) pour bien claire le premier a N terme et le deuxieme n! . et pour misterayoub : je n'ai auccune idéé  | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Dim 21 Aoû 2011, 17:27 Dim 21 Aoû 2011, 17:27 | |
| - Misterayyoub a écrit:
- deux petites questions ,
1) 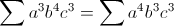 ?? puisqu'il ne joue qu'un role cyclique si on developpe le tout , on aura la meme cigma cyclique , je me demande si c vrai, la meme chose pour celle ci : ?? puisqu'il ne joue qu'un role cyclique si on developpe le tout , on aura la meme cigma cyclique , je me demande si c vrai, la meme chose pour celle ci :
2)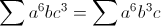 ??? ??? Bonjour, selon ce que je sais: En ce qui concerne la somme cyclique: =f(a,b,c)+f(b,c,a)+f(c,a,b)) 1) 1)  Donc, on constate que:  2) 2) Voyons la deuxième:   Donc, maintenant, il est clair que:  Quant à la somme symétrique, elle est l'ensemble des permutations de {1,2,...,n}, c'est à dire il y a n! termes. Et par conséquent, si on l'applique sur la question 2, on aura bien:  Sauf erreur. | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Dim 21 Aoû 2011, 17:29 Dim 21 Aoû 2011, 17:29 | |
|
Dernière édition par kaj mima le Lun 22 Aoû 2011, 00:18, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Dim 21 Aoû 2011, 17:38 Dim 21 Aoû 2011, 17:38 | |
| Le sigma symétrique veut dire faire des permutations symétrique pour tout les p-uplets.
Pour le sigma cyclique le nombre de termes est égal au nombre des variables et on suit juste un cycle a_1=>a_2=>...=>a_n=>a_1. | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Lun 22 Aoû 2011, 00:35 Lun 22 Aoû 2011, 00:35 | |
| coucou kaj mima  ! peux-tu donner un peu plus de détails à propos de l'exemple :sum(sym)de a ,je ne le saisis toujours pas, et merci d'avance  | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Lun 22 Aoû 2011, 00:38 Lun 22 Aoû 2011, 00:38 | |
| - kaj mima a écrit:
Quant à la somme symétrique, elle est l'ensemble des permutations de {1,2,...,n}, c'est à dire il y a n! termes.
=f(a,b,c)+f(b,a,c)+f(c,a,b)+f(a,c,b)+f(b,c,a)+f(c,b,a)) On peut écrire:  Donc: ) Et voilà! J'espère que c'est clair maintenant. | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  Lun 22 Aoû 2011, 00:41 Lun 22 Aoû 2011, 00:41 | |
| oui , c'est vraiment clair maintenant ,mercii  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Pour en etre sur ! Sujet: Re: Pour en etre sur !  | |
| |
|
  | |
| | Pour en etre sur ! |  |
|
