ali-mes
Expert sup
 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 | | Sujet: Inégalité géométrique Dim 04 Sep 2011, 05:44 | |
| Soit ABC un triangle, dont le périmètre est 1.
on note D, E et F les pieds des bissectrices issues des sommets A, B et C respectivement.
Trouver le max de: AD+BE+CF. | |
|
Mehdi.O
Expert sup
Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
| | Sujet: Re: Inégalité géométrique Dim 04 Sep 2011, 06:16 | |
| Solution : On démontre tout d'abord le lemme suivant : Lemme: Soit ABC un triangle et D le pied issu de la bissectrice de l'angle {BAC}. Nous avons : ^2})}) . Preuve :Par le théorème de la bissectrice intérieure nous avons : 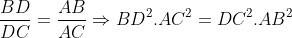 . Mais par Al-Kashi nous avons : },&space;DC^{2}=AD^{2}+AC^{2}-2AD.AC.\textup{cos(x)}) où x=1/2angle{BAC}. Ainsi : })AC^2=(AD^2+AC^2-2AD.AC.\textup{cos(x)})AB^2\Rightarrow&space;AD^2(AC+AB)=2AD.AB.AC.\textup{cos(x)}\Rightarrow&space;AD^{2}=\frac{4AB^2.AC^2.\textup{cos}^{2}(x)}{(AC+AB)^{2}}=AB.AC.\frac{AB^2+AC^2+2AB.AC-AB^2-AC^2+2AB.AC.\textup{cos(2x)}}{AC+AB)^{2}}=AB.AC.(1-(\frac{BC}{AB+AC})^{2})) . Fin de la preuve du lemme.Revenons à notre inégo : On pose a=BC et b=AC et c =AB la condition est équivalente à a+b+c=1. Et l'inégo à : ^{2})}\leq&space;\sum&space;\sqrt{(\frac{(b+c^2)}{4}).(1-(\frac{a}{b+c})^{2})}=\frac{1}{2}\sum&space;\sqrt{{(1-a)^{2}-a^2}}=\frac{1}{2}\sum&space;\sqrt{1-2a}\leq&space;\frac{1}{2}\sqrt{3(3-2(\sum&space;a))}=\frac{\sqrt{3}}{2}) . Ainsi le maximum est : 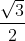 . Egalité si et seulement si le triangle est équilatéral. | |
|
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Inégalité géométrique Dim 04 Sep 2011, 08:21 | |
| Joli, votre preuve est quasiment similaire à la mienne, sauf que j'ai démontré autrement le lemme, et voici ma démonstration: (j'utilise les notations qu'a utilisé Mehdi.O) On a:  . ) . &space;}\Rightarrow&space;AD=\frac{2\sin&space;x&space;.&space;\cos&space;x&space;.&space;AB&space;.&space;AC}{\sin&space;x&space;.&space;(AB+AC)}) . }\Rightarrow&space;AD=\frac{2&space;\cos&space;\left&space;(&space;\frac{A}{2}&space;\right&space;).bc}{b+c}) . (*) Et on a: -(p-b)(p-c)=p^2-pa-p^2+pb+pc-bc=p(b+c-a)-bc) . -(p-b)(p-c)=\frac{1}{2}(a+b+c)(b+c-a)-bc=\frac{1}{2}((b+c)^2-a^2)-bc) . -(p-b)(p-c)=\frac{1}{2}(b^2+c^2+2bc-a^2)-bc=\frac{b^2+c^2-a^2}{2}=bc.&space;\cos&space;A\;&space;\;&space;\;&space;\;&space;\mathrm{D'apr\grave{e}s}&space;\;&space;\;&space;\mathrm{Al-Kashi}) . (1) Et on a: +(p-b)(p-c)=p^2-pa+p^2-pb-pc+bc=2p^2-p(a+b+c)+bc=2p^2-p\times&space;2p+bc=2p^2-2p^2+bc=bc) . (2) (1)+(2)=> =bc(1+\cos&space;A)\Rightarrow&space;p(p-a)=bc\left&space;(\frac{1+&space;\cos&space;A}{2}&space;\right&space;)=bc.&space;\cos^2&space;\left&space;(&space;\frac{A}{2}&space;\right&space;)\Rightarrow&space;cos\left&space;(&space;\frac{A}{2}&space;\right&space;)=\sqrt{\frac{p(p-a)}{bc}}) . On remplace dans (*), on trouve: }{bc}}\times&space;\frac{bc}{b+c}=2\frac{\sqrt{bc.p(p-a)}}{b+c}\Rightarrow&space;AD^2=4bc\frac{p(p-a)}{(b+c)^2}=bc\frac{4p(p-a)}{(b+c)^2}=bc\frac{4(\frac{a+b+c}{2})(\frac{b+c-a}{2})}{(b+c)^2}=bc\frac{(b+c)^2-a^2}{(b+c)^2}=bc\left&space;(&space;1-\left&space;(&space;\frac{a}{b+c}&space;\right&space;)^2&space;\right&space;)) . Et enfin,  ! | |
|
Contenu sponsorisé
| | Sujet: Re: Inégalité géométrique | |
| |
|
