| | Olympiade Terminale 09/12/2011 |  |
|
+4boubou math idemon yasserito medtaha 8 participants |
| Combien d'exos t'as fait ??? | | 1 | | 0% | [ 0 ] | | 2 | | 53% | [ 8 ] | | 3 | | 33% | [ 5 ] | | 4 | | 13% | [ 2 ] |
| | Total des votes : 15 | | | |
|
| Auteur | Message |
|---|
medtaha
Féru

 Nombre de messages : 32 Nombre de messages : 32
Age : 29
Localisation : Casablanca
Date d'inscription : 30/10/2010
 |  Sujet: Olympiade Terminale 09/12/2011 Sujet: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 10:11 Sam 10 Déc 2011, 10:11 | |
| <script src='http://img850.imageshack.us/shareable/?i=olympiade.png&p=tl' type='text/javascript'></script><noscript>  </noscript> | |
|
  | |
medtaha
Féru

 Nombre de messages : 32 Nombre de messages : 32
Age : 29
Localisation : Casablanca
Date d'inscription : 30/10/2010
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 10:14 Sam 10 Déc 2011, 10:14 | |
| au premier il suffit de trouver les facteurs du polynome
au troizieme faut montrer que f est injective et puis trouver que f est -x+1 ou x-1/3 | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 13:10 Sam 10 Déc 2011, 13:10 | |
| tu peux me donner une solution detaillée de l'exercice 3?
N.B: (x-1/3) n'appartient pas a Z. | |
|
  | |
idemon
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 29
Date d'inscription : 03/12/2011
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 13:37 Sam 10 Déc 2011, 13:37 | |
| Quelqu'un a une idée pour le 2? | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 13:56 Sam 10 Déc 2011, 13:56 | |
| - yasserito a écrit:
- tu peux me donner une solution detaillée de l'exercice 3?
N.B: (x-1/3) n'appartient pas a Z. SOLUTION,exo3 d'abord,on remarque que f est injective prouvons cela pour tous a,b dans Z f(a)=f(b) --> 2f(a)=f(a)+f(b) ----> f(2f(a))=f(f(a)+f(b))---> 2a=a+b---> a=b d'ou l'injectivité de f d'une autre part f(2f(a))=2a-1 et f(f(a-1)+f(a+1))=2a-1 , l'injectivité de f implique 2f(a)=f(a-1)+f(a+1) un récurrence directe nous permet d'affirmer que f est affine en remplaçons dans l’équation du début,il nous que la seul fonction affine qui satisfait les conditions de l'énoncé est f(x)=-x+1 | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 14:04 Sam 10 Déc 2011, 14:04 | |
| - boubou math a écrit:
- yasserito a écrit:
- tu peux me donner une solution detaillée de l'exercice 3?
N.B: (x-1/3) n'appartient pas a Z. SOLUTION,exo3
d'abord,on remarque que f est injective prouvons cela
pour tous a,b dans Z
f(a)=f(b) --> 2f(a)=f(a)+f(b) ----> f(2f(a))=f(f(a)+f(b))---> 2a=a+b---> a=b
d'ou l'injectivité de f
d'une autre part
f(2f(a))=2a-1 et f(f(a-1)+f(a+1))=2a-1 , l'injectivité de f implique
2f(a)=f(a-1)+f(a+1)
un récurrence directe nous permet d'affirmer que f est affine
en remplaçons dans l’équation du début,il nous que la seul fonction affine qui satisfait les conditions de l'énoncé est f(x)=-x+1 wee,c vrai,merci pour la solution  | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 14:34 Sam 10 Déc 2011, 14:34 | |
| Bonjour
L'énoncé ainsi que les solutions sont disponibles à cette adresse | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 14:52 Sam 10 Déc 2011, 14:52 | |
| - idemon a écrit:
- Quelqu'un a une idée pour le 2?
Je présente ma solution à l'inégalité durant le test : Solution au problème 2 :On pose x=(1-a)/a et y=(1-b)/b et z= (1-c)/c. La condition devient xy+xz+yz=xyz. On pose p=x+y+z et q=xy+xz+yz=xyz L'inégalité devient équivalente à 2q>=5p+9, mais puisque q²>=3qp => q>=3p. Ainsi il suffit de prouver que p>=9 qui est immédiat par CS vu que 1/x+1/y+1/z=1. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 18:16 Sam 10 Déc 2011, 18:16 | |
| - boubou math a écrit:
- yasserito a écrit:
- tu peux me donner une solution detaillée de l'exercice 3?
N.B: (x-1/3) n'appartient pas a Z. SOLUTION,exo3
d'abord,on remarque que f est injective prouvons cela
pour tous a,b dans Z
f(a)=f(b) --> 2f(a)=f(a)+f(b) ----> f(2f(a))=f(f(a)+f(b))---> 2a=a+b---> a=b
d'ou l'injectivité de f
d'une autre part
f(2f(a))=2a-1 et f(f(a-1)+f(a+1))=2a-1 , l'injectivité de f implique
2f(a)=f(a-1)+f(a+1)
un récurrence directe nous permet d'affirmer que f est affine
en remplaçons dans l’équation du début,il nous que la seul fonction affine qui satisfait les conditions de l'énoncé est f(x)=-x+1 Svp,pour la recurrence,comment vous avez fait pour la premier valeur ainsi que ta facon d'avancer cette recurrence en Z? | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 18:40 Sam 10 Déc 2011, 18:40 | |
| A vrai dire je doute qu'une récurrence soit possible sur Z tout entier. Voici ma solution : Soient 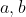 des entiers et soit ) la relation de l'équation fonctionnelle. \Rightarrow%20f(2f(a))=2a-1) et il s'ensuit que  est injective. Or, P(a,b) et P(a+b,0) nous donnent par l'injectivité f(a)+f(b)=f(a+b)+f(0) Et en ajoutant -2f(0) de part et d'autre nous avons f(a)-f(0)+f(b)-f(0)=f(a+b)-f(0) Et donc la fonction g définie pour tout entier c par g(c)=f(c)-f(0) vérifie la classique équation fonctionnelle de Cauchy. Ainsi il existe une constante k telle que g(a)=k.a d'où f(a)=k.a+f(0). Et en insérant cette fonction dans la relation initiale on doit avoir k=-1 et f(0)=1. Ainsi f(a)=1-a. Cette dernière fonction vérifié bien la relation de l'équation fonctionnelle  | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 18:48 Sam 10 Déc 2011, 18:48 | |
| comme recurrence en Z, ca nous pose pas de probleme car on peut la demontrer sur IN puis sur IN- en trouvant une relation entre f(n) et f(-n) ce qui est facile en prenant b=-a. Mais pour la premiere valeur de recurrence,faut un peu d'eclairssisement. En ce qui concerne ta solution momo, elle est tres bonne,j'ai reussi a prouver que f(a)+f(b)=f(a+b)+f(0),mais je n'ai pas reussi a la developper en suite de cauchy surtout que je l'ai oublié. Merci pour ta solution  | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 19:09 Sam 10 Déc 2011, 19:09 | |
| Pas de quoi ^^ Et figure toi que je suis dans le même cas de figure que toi  Il y a aussi ce problème qui ressemble pas mal à celui qui nous a été proposé. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 19:12 Sam 10 Déc 2011, 19:12 | |
| - momo1729 a écrit:
- Pas de quoi ^^
Et figure toi que je suis dans le même cas de figure que toi 
Il y a aussi ce problème qui ressemble pas mal à celui qui nous a été proposé.
Manque d'hypothèses dans l'utilisation de l'équation de Caushy. | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Sam 10 Déc 2011, 19:22 Sam 10 Déc 2011, 19:22 | |
| On ne manque d'hypothèses que si on travaille sur R tout entier : il faut alors des conditions comme la continuité ou la monotonie. Sur Q, la solution proposée est bien la seule. Et c'est donc bien le cas dans notre problème puisqu'on raisonne dans Z.
Je te redirige vers Wikipédia | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Dim 11 Déc 2011, 11:19 Dim 11 Déc 2011, 11:19 | |
| - yasserito a écrit:
- boubou math a écrit:
- yasserito a écrit:
- tu peux me donner une solution detaillée de l'exercice 3?
N.B: (x-1/3) n'appartient pas a Z. SOLUTION,exo3
d'abord,on remarque que f est injective prouvons cela
pour tous a,b dans Z
f(a)=f(b) --> 2f(a)=f(a)+f(b) ----> f(2f(a))=f(f(a)+f(b))---> 2a=a+b---> a=b
d'ou l'injectivité de f
d'une autre part
f(2f(a))=2a-1 et f(f(a-1)+f(a+1))=2a-1 , l'injectivité de f implique
2f(a)=f(a-1)+f(a+1)
un récurrence directe nous permet d'affirmer que f est affine
en remplaçons dans l’équation du début,il nous que la seul fonction affine qui satisfait les conditions de l'énoncé est f(x)=-x+1
Svp,pour la récurrence,comment vous avez fait pour la premier valeur ainsi que ta facon d'avancer cette recurrence en Z? on effet, on va procéder par 2 récurrences fortes, une sur les entiers positif et une autre sur les négatifs pour prouver que f(a)=a[f(1)-f(0)]+f(0).cela affirme que f est affine | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Dim 11 Déc 2011, 12:37 Dim 11 Déc 2011, 12:37 | |
| - boubou math a écrit:
- Spoiler:
- yasserito a écrit:
- boubou math a écrit:
- yasserito a écrit:
- tu peux me donner une solution detaillée de l'exercice 3?
N.B: (x-1/3) n'appartient pas a Z. SOLUTION,exo3
d'abord,on remarque que f est injective prouvons cela
pour tous a,b dans Z
f(a)=f(b) --> 2f(a)=f(a)+f(b) ----> f(2f(a))=f(f(a)+f(b))---> 2a=a+b---> a=b
d'ou l'injectivité de f
d'une autre part
f(2f(a))=2a-1 et f(f(a-1)+f(a+1))=2a-1 , l'injectivité de f implique
2f(a)=f(a-1)+f(a+1)
un récurrence directe nous permet d'affirmer que f est affine
en remplaçons dans l’équation du début,il nous que la seul fonction affine qui satisfait les conditions de l'énoncé est f(x)=-x+1
Svp,pour la récurrence,comment vous avez fait pour la premier valeur ainsi que ta facon d'avancer cette recurrence en Z?
on effet, on va procéder par 2 récurrences fortes, une sur les entiers positif et une autre sur les négatifs pour prouver que f(a)=a[f(1)-f(0)]+f(0).cela affirme que f est affine We... c'est ca! | |
|
  | |
youpousou
Débutant
 Nombre de messages : 4 Nombre de messages : 4
Age : 30
Date d'inscription : 05/12/2011
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Lun 12 Déc 2011, 19:03 Lun 12 Déc 2011, 19:03 | |
| Solution 1 exo:  | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  Lun 19 Déc 2011, 00:10 Lun 19 Déc 2011, 00:10 | |
| Pour le 2 : On a 0<a<1 donc il existe x>0 tq 1/a-1=3/x donc on peut poser a=x/(3+x) la condition devient x+y+z=3 et l'inégalité devient \sum x/(3+x)=<3/4 pour cela on utilise le lemme suivant : (3x+1)/16>=x/(3+x) DOne! - Spoiler:
le lemme peut etre démontrer ainsi :1+1+1+1/x>=16/(x+3) Via L7aj Cauchy, Une multilicaiton par x terminera l'affaire
Bonne chance à vous . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiade Terminale 09/12/2011 Sujet: Re: Olympiade Terminale 09/12/2011  | |
| |
|
  | |
| | Olympiade Terminale 09/12/2011 |  |
|
