|
| | trouver tous x,y |  |
| | | Auteur | Message |
|---|
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: trouver tous x,y Sujet: trouver tous x,y  Dim 12 Fév 2012, 18:21 Dim 12 Fév 2012, 18:21 | |
| Trouver tous les entiers x,y tels que :
x^3+y^3+x²y+y²x=8(x²+y²+xy+1) | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: trouver tous x,y Sujet: Re: trouver tous x,y  Mar 14 Fév 2012, 20:21 Mar 14 Fév 2012, 20:21 | |
| - diablo902 a écrit:
- Trouver tous les entiers x,y tels que :
x^3+y^3+x²y+y²x=8(x²+y²+xy+1) L'équation proposée est équivalente à (x^2+y^2)=4(x+y)^2+4(x^2+y^2+2)) . On pose, en guise de simplification, 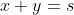 et 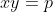 . On a donc ^2-2xy=s^2-2p) . L'équation s'écrit encore =4s^2+4(s^2-2p+2)) . Ou encore 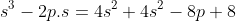 . Et cela veut dire 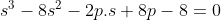 .==>(*) Cette relation implique que  est un entier pair. D'où l'existence d'un entier  tel que 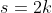 . Lorsqu'on reprends dans l'équation, on tombe sur 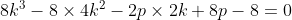 ou encore sur 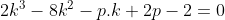 . On écrit l'équation de la manière suivante =2k^3-8k^2-2) . On obtient ainsi =2k^2.(k-2)-4k.(k-2)-8(k-2)-18) . Ce qui veut dire que 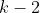 divise 18. Ainsi 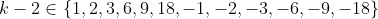 . Et 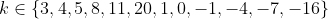 . Donc 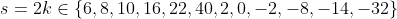 . On se ramène tout simplement vers une distinction marrante de cas: On prends un entier de l'ensemble précédent et on le remplace dans *. Lorsqu'on calcule p, on se ramène à rsoudre l'équation 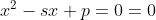 . Si le discriminent est négatif ou n'est pas un carré parfait, on n'aura plus de solutions. On a les résultats suivants: ***Si s=6, on aura 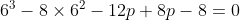 . Donc 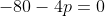 , donc 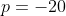 . On a =36+80=116) , qui n'est pas un carré parfait. Il n'y a pas de solutions dans ce cas. ***Si s=8, on aura 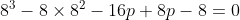 . Donc 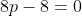 , donc 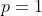 . On a 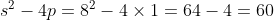 , qui n'est pas un carré parfait. Il n'y a pas de solutions dans ce cas. ***Si s=10, on aura 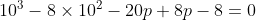 . Donc 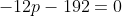 , donc 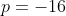 . On a =100+64=164) , qui n'est pas un carré parfait. Il n'y a pas de solutions dans ce cas. ***Si s=16, on aura 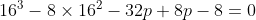 . Donc 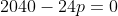 , donc 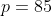 . On a 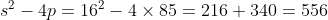 , qui n'est pas un carré parfait. Il n'y a pas de solutions dans ce cas. ***Si s=22, on aura 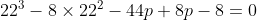 . Donc 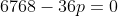 , donc 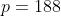 . On a 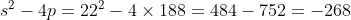 , qui est négatif. Il n'y a pas de solutions dans ce cas. ***Si s=40, on aura 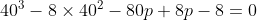 . Donc 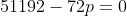 , donc 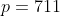 . On a 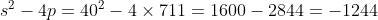 , qui est négatif. Il n'y a pas de solutions dans ce cas. ***Si s=2, on aura 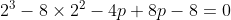 . Donc 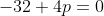 , donc 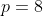 . On a 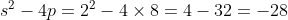 , qui est négatif. Il n'y a pas de solutions dans ce cas. ***Si s=0, on aura 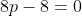 . Donc 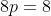 , donc 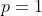 . On a 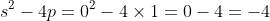 , qui est négatif. Il n'y a pas de solutions dans ce cas. ***Si s=-2, on aura ^3-8\times(-2)^2+4p+8p-8=0) . Donc 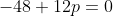 , donc 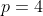 . On a ^2-4\times4=4-16=-12) , qui est négatif. Il n'y a pas de solutions dans ce cas. ***Si s=-8, on aura ^3-8\times(-8 )^2+16p+8p-8=0) . Donc 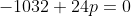 , donc 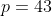 . On a ^2-4\times43=64-172=108) , qui n'est pas un carré parfait. Il n'y a pas de solutions dans ce cas. ***Si s=-14, on aura ^3-8\times(-14)^2+28p+8p-8=0) . Donc 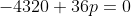 , donc 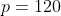 . On a ^2-4\times120=196-480=-284) , qui est négatif. Il n'y a pas de solutions dans ce cas. ***Si s=-32, on aura ^3-8\times(-32)^2+64p+8p-8=0) . Donc 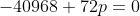 , donc 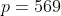 . On a ^2-4\times569=1024-2276=-1252) , qui est négatif. Il n'y a pas de solutions dans ce cas. ***Synthèse: le problème proposé n'admet aucune solution entière. Sauf erreurs. J'ai perdu beaucoup de temps en cherchant comment diminuer les cas, mais en vain. J'attends vos critiques et vos solutions alternatives. | |
|   | | Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: trouver tous x,y Sujet: Re: trouver tous x,y  Mer 15 Fév 2012, 12:20 Mer 15 Fév 2012, 12:20 | |
| C'est clair que tu as perdu beaucoup de temps x)
Moi j'avais essayé de simplifier et diminuer les cas, mais je trouvais qu'il y a 32 cas avec plusieurs sous cas donc j'ai arreté. Je crois qu'il y a donc erreur dans l'ennoncé... | |
|   | | diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: trouver tous x,y Sujet: Re: trouver tous x,y  Jeu 16 Fév 2012, 18:20 Jeu 16 Fév 2012, 18:20 | |
| - nmo a écrit:
- diablo902 a écrit:
- Trouver tous les entiers x,y tels que :
x^3+y^3+x²y+y²x=8(x²+y²+xy+1) L'équation proposée est équivalente à (x^2+y^2)=4(x+y)^2+4(x^2+y^2+2)) . .
On pose, en guise de simplification, 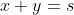 et et 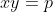 . .
On a donc ^2-2xy=s^2-2p) . .
L'équation s'écrit encore =4s^2+4(s^2-2p+2)) . .
Ou encore 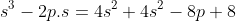 . .
Et cela veut dire 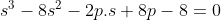 .==>(*) .==>(*)
Cette relation implique que  est un entier pair. est un entier pair.
D'où l'existence d'un entier  tel que tel que 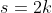 . .
Lorsqu'on reprends dans l'équation, on tombe sur 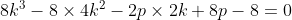 ou encore sur ou encore sur 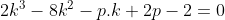 . .
On écrit l'équation de la manière suivante =2k^3-8k^2-2) . .
On obtient ainsi =2k^2.(k-2)-4k.(k-2)-8(k-2)-18) . .
Ce qui veut dire que 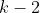 divise 18. divise 18.
Ainsi 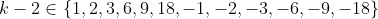 . .
Et 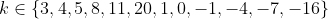 . .
Donc 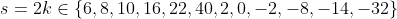 . .
On se ramène tout simplement vers une distinction marrante de cas:
On prends un entier de l'ensemble précédent et on le remplace dans *.
Lorsqu'on calcule p, on se ramène à rsoudre l'équation 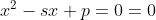 . .
Si le discriminent est négatif ou n'est pas un carré parfait, on n'aura plus de solutions.
On a les résultats suivants:
***Si s=6, on aura 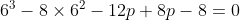 . .
Donc 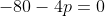 , donc , donc 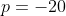 . .
On a =36+80=116) , qui n'est pas un carré parfait. , qui n'est pas un carré parfait.
Il n'y a pas de solutions dans ce cas.
***Si s=8, on aura 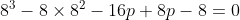 . .
Donc 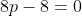 , donc , donc 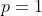 . .
On a 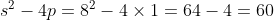 , qui n'est pas un carré parfait. , qui n'est pas un carré parfait.
Il n'y a pas de solutions dans ce cas.
***Si s=10, on aura 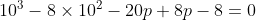 . .
Donc 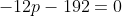 , donc , donc 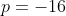 . .
On a =100+64=164) , qui n'est pas un carré parfait. , qui n'est pas un carré parfait.
Il n'y a pas de solutions dans ce cas.
***Si s=16, on aura 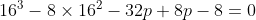 . .
Donc 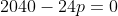 , donc , donc 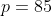 . .
On a 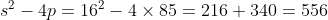 , qui n'est pas un carré parfait. , qui n'est pas un carré parfait.
Il n'y a pas de solutions dans ce cas.
***Si s=22, on aura 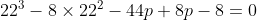 . .
Donc 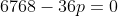 , donc , donc 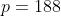 . .
On a 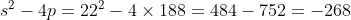 , qui est négatif. , qui est négatif.
Il n'y a pas de solutions dans ce cas.
***Si s=40, on aura 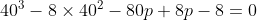 . .
Donc 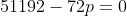 , donc , donc 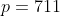 . .
On a 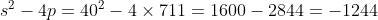 , qui est négatif. , qui est négatif.
Il n'y a pas de solutions dans ce cas.
***Si s=2, on aura 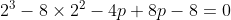 . .
Donc 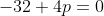 , donc , donc 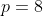 . .
On a 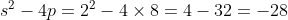 , qui est négatif. , qui est négatif.
Il n'y a pas de solutions dans ce cas.
***Si s=0, on aura 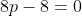 . .
Donc 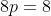 , donc , donc 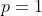 . .
On a 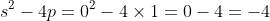 , qui est négatif. , qui est négatif.
Il n'y a pas de solutions dans ce cas.
***Si s=-2, on aura ^3-8\times(-2)^2+4p+8p-8=0) . .
Donc 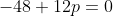 , donc , donc 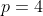 . .
On a ^2-4\times4=4-16=-12) , qui est négatif. , qui est négatif.
Il n'y a pas de solutions dans ce cas.
***Si s=-8, on aura ^3-8\times(-8 )^2+16p+8p-8=0) . .
Donc 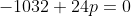 , donc , donc 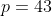 . .
On a ^2-4\times43=64-172=108) , qui n'est pas un carré parfait. , qui n'est pas un carré parfait.
Il n'y a pas de solutions dans ce cas.
***Si s=-14, on aura ^3-8\times(-14)^2+28p+8p-8=0) . .
Donc 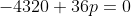 , donc , donc 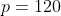 . .
On a ^2-4\times120=196-480=-284) , qui est négatif. , qui est négatif.
Il n'y a pas de solutions dans ce cas.
***Si s=-32, on aura ^3-8\times(-32)^2+64p+8p-8=0) . .
Donc 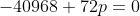 , donc , donc 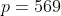 . .
On a ^2-4\times569=1024-2276=-1252) , qui est négatif. , qui est négatif.
Il n'y a pas de solutions dans ce cas.
***Synthèse: le problème proposé n'admet aucune solution entière.
Sauf erreurs.
J'ai perdu beaucoup de temps en cherchant comment diminuer les cas, mais en vain.
J'attends vos critiques et vos solutions alternatives. k est un entier(x et y le sont  ) c'est un exercice ImO 1980 | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: trouver tous x,y Sujet: Re: trouver tous x,y  Ven 17 Fév 2012, 17:07 Ven 17 Fév 2012, 17:07 | |
| - diablo902 a écrit:
- k est un entier (x et y le sont
 ) )
c'est un exercice ImO 1980 Ce n'est pas une critique mon cher. Un entier est soit positif, soit négatif. Il faut chercher une autre methode pour diminuer les cas. | |
|   | | Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: trouver tous x,y Sujet: Re: trouver tous x,y  Sam 18 Fév 2012, 16:29 Sam 18 Fév 2012, 16:29 | |
| Bonsoir,
Je viens de trouver enfin la solution:
S = {(2,8);(8,2)}
Je vous laisse donc chercher un peu avant de poster ma méthode,
bonne chance ;) | |
|   | | diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: trouver tous x,y Sujet: Re: trouver tous x,y  Sam 18 Fév 2012, 16:56 Sam 18 Fév 2012, 16:56 | |
| | |
|   | | Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: trouver tous x,y Sujet: Re: trouver tous x,y  Sam 18 Fév 2012, 17:31 Sam 18 Fév 2012, 17:31 | |
| Bonsoir,
diablo902, si ce n'est pas ta solution, pourquoi donc la poster et en anglais en plus ???
Bon, voici ma solution:
On pose x^2+y^2 = a , x+y = b.
Comme nmo, j'ai trouvé que:
b E {6,8,10,16,22,40,2,0,-2,-8,-14,-32}
D'une autre part, l'equation est equivalente à:
a(b-4) = 4b^2 +8 (*) ==> b > 4.
Donc:
b E {6,8,10,16,22,40}
En remplacant dans (*), on trouve que:
Seuls b = 10 / a = 68 peuvent satisfaire la relation, en utilisant les carrés parfaits.
Enfin:
S = {(2,8);(8,2)}
PS: Mon grand frère a trouvé le meme résultat en utilisant la dérivation sur x et sur y. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: trouver tous x,y Sujet: Re: trouver tous x,y  Sam 18 Fév 2012, 20:27 Sam 18 Fév 2012, 20:27 | |
| - diablo902 a écrit:
- J'ai oublié positives. En tout cas votre méthode est fausse

 Non, la methode est bonne. Mais, je me suis trompé dans les calculs. En tout cas, merci pour la solution. | |
|   | | Contenu sponsorisé
 |  Sujet: Re: trouver tous x,y Sujet: Re: trouver tous x,y  | |
| |
|   | | | | trouver tous x,y |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
