Le Grand Defi 1 : Math en pratique !! -Momo-

Bonjours cher amateur de maths,

J'espere que vous vous rappellez les probleme du primaire et combien c'est amusant des les resoudre !!
Aujourdh'ui j'ai pour vous la meme chose mais la on parle du gros calibre : Quelque exercices pour mettre votre math en pratique !!



Amusez vous bien !!

Momo.

C'est pas aussi difficile que ça, Bon j'espere !!

momokani a écrit:

C'est pas aussi difficile que ça, Bon j'espere !!

Ce n'est pas difficile, mais fatiguant.
Voici ce que j'ai fait pour résoudre le a):
Soient les ensembles suivants: , , des nombres coloriés respectivement par le bleu, le vert et le rouge.
Premièrement, il faut signaler que la phrase "la somme de deux nombres en bleu..." cache dedans que les deux nombres sont différents.
Il faut signaler aussi que ces ensembles sont non-vides.
La première hypothèse se traduit par: .
Et la seconde par: .

***On démontre premièrement que 0 est colorié par le vert.
En effet, on a deux cas qui mènent vers une contradiction:
-si 0 est colorié en rouge, 0 serait aussi colorié en bleu (en utilisant la première hypothèse).
-si 0 est colorié en bleu: si a un entier non nul colorié en bleu, alors ce a serait aussi colorié en rouge (en utilisant la deuxième hypothèse).
-On conclut que 0 est colorié en vert.

*** On veut démontrer que le négatif de chaque nombre en bleu est un nombre colorié en rouge.
Cela se traduit par .
Soit un nombre colorié en rouge.
-Supposons par l'absurde que .
En utilisant la deuxième hypothèse, 0 qui est la somme de x et -x, serait colorié en rouge.
Ce qui contredit le premier résultat.
-Supposons par l'absurde que .
Maintenant, si y est un entier colorié en bleu, on doit avoir x+y un entier colorié en rouge.
Ainsi -x-y est colorié en bleu (en utilisant la deuxième hypothèse).
Donc -y, qui est la somme de deux nombres colorié en bleu x et -x-y, doit être colorié en rouge.
Ce qui vient en contradiction avec ce qu'on a supposé.

*** On veut démontrer que la somme de deux entiers coloriés en rouge est un nombre colorié en bleu.
Cela se traduit par .
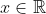
Soit et deux nombres coloriés en rouge.
-Supposons par l'absurde que .
En utilisant la première hypothèse, -x et -y seraient coloriés en bleu.
Et donc l'entier -x-y serait colorié en rouge.
Du coup, x+y doit être colorié en bleu.
Ce qui contredit la supposition.
-Supposons par l'absurde que .
De la même manière que précédemment, on aboutit à x+y est colorié en bleu.
Ce qui contredit la supposition.

CQFD.
Sauf erreur.

Chapeau !! J'ai fait presque la meme chose !!
Je pense que c'est un interessant pratique pour les eleves du 1er Bac (Ensemble)
Pourtant j'ai pas vraiment compris la dexieme question !! si quelqu'un a une idée de quoi il s'agit vraiment

Je complète mon travail en résolvant le b):
On a les 5 résultats suivants:
1) Le négatif d'un nombre colorié en rouge est un nombre colorié en bleu.
2) La somme de deux nombres coloriés en rouge est un nombre colorié en bleu.
3) Le négatif d'un nombre colorié en bleu est un nombre colorié en rouge.
4) La somme de deux nombres coloriés en bleu est un nombre colorié en rouge.
5) 0 est colorié en vert.
On doit utiliser ces résultats pour trouver les colorations possibles:
je dois dire que si un nombre coloriés en vert, alors son négatif est de la même couleur.
(Ce résultat découle immédiatement des quatres premiers résultats ci-cités).

***Le premier cas: 1 est coloriés en rouge.
Alors, -1 est coloriés en bleu.
On distingue maintenant trois sous-cas:
*Si 2 est coloriés en rouge.
On aura -2 est coloriés en bleu.
Puisque 3=2+1, 3 est coloriés en bleu. Ainsi -3 est coloriés en rouge.
4 est colorié en vert, car sinon on aura contradiction.
En effet, si 4 est colorié en bleu alors 3=4+(-1) doit être colorié en rouge.
Ce qui contredit le fait que 3 est colorié en bleu.
Et si 4 est colorié en rouge alors 1=4+(-3) doit être colorié en bleu.
Ce qui contredit le fait que 3 est colorié en rouge.
Du coup, -4 est lui aussi colorié en vert.
Un raisonnement analogue, montre que tous les nombres qui viennent après 4 (5,6,...) et -4 (-5,-6,...) sont coloriés en vert.
D'où la première coloration possible.
*Si 2 est coloriés en bleu.
On aura -2 est colorié en rouge.
Par symétrie à la situation précédante (1 et 2 prennent le rôle de 2 et 3 respectivement), tous les nombres autre que 1,2,-1 et -2 doivent être coloriés en vert.
D'où la deuxième coloration possible.
*Si 2 est colorié en vert.
On aura -2 est colorié en vert.
3 est colorié soit en vert , soit en rouge, car sinon on aura contradiction.
En effet, si 3 est colorié en bleu alors 2=3+(-1) doit être colorié en rouge.
Ce qui contredit le fait que 2 est colorié en vert.
--Si 3 est colorié en rouge, on aura -3 est colorié en bleu.
De plus, 4=3+1 doit être colorié en bleu. Et par conséquent -4 est colorié en rouge.
-Si 5 est colorié en bleu, alors 2=5+(-3) doit être colorié en rouge, ce qui constitue une contradiction avec la couleur de 2 qui est verte.
-Si 5 est colorié en rouge, alors 1=5+(-4) doit être colorié en bleu, ce qui est contradictoire avec l'hypothèse du premier cas qu'on étudie.
Il s'avère que 5 est colorié en vert, et son négatif qui est -5 l'est également.
Un raisonnement analogue, montre que tous les nombres qui viennent après 5 (6,7,...) et -5 (-6,-7,...) sont coloriés en vert.
D'où la troisième coloration possible.
--Si 3 est colorié en vert, on aura -3 est colorié en vert.
Ici, on remarque que ce 3 va jouer le rôle de 2 colorié en vert.
On se ramène donc à deux cas: ou bien 4 est colorié en rouge, ou bien 4 est colorié en vert.
Pour le premier cas, on trouvera que 5 est colorié en bleu et -5 doit être colorié en rouge et tous les autres nombres doivent être colorié en vert.
D'où la quatrième coloration possible.
Pour le second cas, on se trouve devant deux cas tel que la situation pécédante.
Et le truc continue comme ça, et je ne peut pas conclure.
Ainsi termine le premier cas.