younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mer 24 Oct 2012, 10:29 Mer 24 Oct 2012, 10:29 | |
| - nmo a écrit:
- Oty a écrit:
- soit a,b,c >=0 tel que : ab+bc+ca=3 , Prouver que :
 . . J'ai voulu rédiger cette solution vers midi, mais l'ordinateur s'est redémarré inopinément!
Le même sort il y a quelques minutes...
Mais, vu que personne n'a fait ce que j'ai en tête, je le partage encore une fois:
Je distingue deux cas:
*Si l'une des variables est nulle:
On suppose par symétrie qu'on a c=0, la contrainte se réduit à ab=3, et on doit démontrer que  . .
Cette inégalité équivaut à 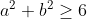 . .
Ce qui est trivialement vrai d'après l'inégalité arithmético-géométrique.
*Si aucune des variables n'est nulle:
On pose premièrement: 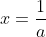 , , 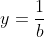 et et 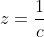 . .
Donc 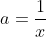 , , 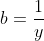 et et 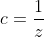 . .
La contrainte devient 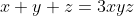 . .
Et l'inégalité, quant à elle, devient: 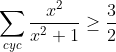 . .
On songe à l'inégalité de Jensen.
On considère la fonction f définie par: =\frac{x^2}{x^2+1}) . .
La fonction f est dérivable sur l'ensemble des réels, et sa fonction dérivée:  ^2}) . .
La fonction f' est dérivable sur l'ensemble des réels, et on a: =\frac{2(1-x)^2}{(x^2+1)^3}) . .
Puisque f'' est positive ou nulle, on déduit que f est une fonction convexe. On peut donc appliquer l'inégalité de Jensen: \ge f(\sum_{cyc}\frac{1}{3}x})) . .
Soit ^2}{(\frac{x+y+z}{3})^2+1}=1-\frac{1}{(xyz)^2+1}) . ==>(1) . ==>(1)
D'un autre côté, on a selon l'inégalité arithmético-géométrique: ^{\frac{1}{3}}) . .
Ce qui veut bien dire que ^2\ge1) . .
Une simple manipulation nous emmène vers ^2+1}\ge\frac{1}{2}) . ==>(2) . ==>(2)
De 1 et 2, on conclut que 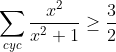 . .
*Les cas d'égalité:
On déduit que notre inégalité devient une égalité si et seulement si:
_Tous les variables valent 1 (Le second cas).
_Une variable est nulle et les deux autres valent  . .
CQFD.
Sauf erreurs. salut vous avez ecrit La fonction f' est dérivable sur l'ensemble des réels, et on a: =\frac{2(1-x)^2}{(x^2+1)^3}) . Puisque f'' est positive ou nulle, on déduit que f est une fonction convexe. ce qui est totalement faux car =\frac{2(1-3x^{2})}{(1+x^{2})^{3}}) donc votre reponse est fausse Mr "nmo" mais elle reste belle ideé!!! | |
|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mer 24 Oct 2012, 23:04 Mer 24 Oct 2012, 23:04 | |
| - younesmath2012 a écrit:
- nmo a écrit:
- Oty a écrit:
- soit a,b,c >=0 tel que : ab+bc+ca=3 , Prouver que :
 . . J'ai voulu rédiger cette solution vers midi, mais l'ordinateur s'est redémarré inopinément!
Le même sort il y a quelques minutes...
Mais, vu que personne n'a fait ce que j'ai en tête, je le partage encore une fois:
Je distingue deux cas:
*Si l'une des variables est nulle:
On suppose par symétrie qu'on a c=0, la contrainte se réduit à ab=3, et on doit démontrer que  . .
Cette inégalité équivaut à 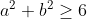 . .
Ce qui est trivialement vrai d'après l'inégalité arithmético-géométrique.
*Si aucune des variables n'est nulle:
On pose premièrement: 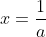 , , 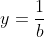 et et 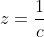 . .
Donc 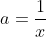 , , 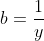 et et 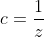 . .
La contrainte devient 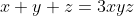 . .
Et l'inégalité, quant à elle, devient: 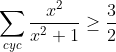 . .
On songe à l'inégalité de Jensen.
On considère la fonction f définie par: =\frac{x^2}{x^2+1}) . .
La fonction f est dérivable sur l'ensemble des réels, et sa fonction dérivée:  ^2}) . .
La fonction f' est dérivable sur l'ensemble des réels, et on a: =\frac{2(1-x)^2}{(x^2+1)^3}) . .
Puisque f'' est positive ou nulle, on déduit que f est une fonction convexe. On peut donc appliquer l'inégalité de Jensen: \ge f(\sum_{cyc}\frac{1}{3}x})) . .
Soit ^2}{(\frac{x+y+z}{3})^2+1}=1-\frac{1}{(xyz)^2+1}) . ==>(1) . ==>(1)
D'un autre côté, on a selon l'inégalité arithmético-géométrique: ^{\frac{1}{3}}) . .
Ce qui veut bien dire que ^2\ge1) . .
Une simple manipulation nous emmène vers ^2+1}\ge\frac{1}{2}) . ==>(2) . ==>(2)
De 1 et 2, on conclut que 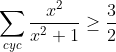 . .
*Les cas d'égalité:
On déduit que notre inégalité devient une égalité si et seulement si:
_Tous les variables valent 1 (Le second cas).
_Une variable est nulle et les deux autres valent  . .
CQFD.
Sauf erreurs. salut vous avez ecrit La fonction f' est dérivable sur l'ensemble des réels, et on a: =\frac{2(1-x)^2}{(x^2+1)^3}) . .
Puisque f'' est positive ou nulle, on déduit que f est une fonction convexe.
ce qui est totalement faux car =\frac{2(1-3x^{2})}{(1+x^{2})^{3}})
donc votre reponse est fausse Mr "nmo" mais elle reste belle ideé!!! J'ai vérifié avec wolfram alpha! Et tu avais raison, Ma solution est déjà dite fausse... | |
|
