| | Inégalité (3) |  |
|
+3abdelbaki.attioui aymas Oty 7 participants |
|
| Auteur | Message |
|---|
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Inégalité (3) Sujet: Inégalité (3)  Lun 20 Aoû 2012, 17:27 Lun 20 Aoû 2012, 17:27 | |
| soit a,b,c >=0 tel que : ab+bc+ca=3 , Prouver que :  .
Dernière édition par Oty le Lun 20 Aoû 2012, 21:57, édité 1 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Lun 20 Aoû 2012, 20:35 Lun 20 Aoû 2012, 20:35 | |
| est ce que c'est ab+ac+bc=3 ou ab+bc=ac=3 | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Lun 20 Aoû 2012, 20:37 Lun 20 Aoû 2012, 20:37 | |
| car le deusieme cas l'exo n'est pas difficile puisque on peut calculer a et b en fonction de c et on réduit l'expression a un polynome | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Lun 20 Aoû 2012, 21:57 Lun 20 Aoû 2012, 21:57 | |
| c'est edité  | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 00:35 Mar 21 Aoû 2012, 00:35 | |
| | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 00:36 Mar 21 Aoû 2012, 00:36 | |
| | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 00:53 Mar 21 Aoû 2012, 00:53 | |
| \sum 1\1+a² >= \sum 1\(1+ab) c'est faux , ton leme est juste seulement si ab >=1 | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 01:18 Mar 21 Aoû 2012, 01:18 | |
|
b=1/(2a) ==> 2/(ab+1)=4/3 > 1
1/(1+a²)+4a²/(1+4a²) -----> 1 quand a ----> 0+
| |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 01:22 Mar 21 Aoû 2012, 01:22 | |
| - abdelbaki.attioui a écrit:
b=1/(2a) ==> 2/(ab+1)=4/3 > 1
1/(1+a²)+4a²/(1+4a²) -----> 1 quand a ----> 0+ pouvez vous expliquer votre remarque ? merci . | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 02:00 Mar 21 Aoû 2012, 02:00 | |
| peut tu explique d'avantage Oty | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 02:42 Mar 21 Aoû 2012, 02:42 | |
| tu as ecris : \sum 1\(a²+1) >= \sum 1\(1+ab) , comme
1\(a²+1) + 1\(b²+1) >= 2\(1+ab) est equivalente a : (a-b)² (ab-1) >= 0 ainsi cette inégalité est vrait seulement si ab >=1 , mais bc ou ca peuvent etre inferieur a 1 donc cette inégalité n'est pas applicable au autre termes | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 12:59 Mar 21 Aoû 2012, 12:59 | |
| - Oty a écrit:
- abdelbaki.attioui a écrit:
b=1/(2a) ==> 2/(ab+1)=4/3 > 1
1/(1+a²)+4a²/(1+4a²) -----> 1 quand a ----> 0+ pouvez vous expliquer votre remarque ? merci . Juste un contre exemple : 1/(1+a²+1/(1+b²)<2/(ab+1) pour ab=1/2 et a assez petit | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 16:07 Mar 21 Aoû 2012, 16:07 | |
|
J'espère pas d'erreur
a, b, c>=0 et ab+ac+bc=3
1/(1+a²)+1/(1+b²)+1/(1+c²)>=3/2
<==> 2 ((1+b²)(1+c²)+(1+a²)(1+c²)(1+b²)(1+a²))>=3(1+a²)(1+b²)(1+c²)
<==> 2 (3+ 2(a²+b²+c²)+ a²b²+a²c²+b²c²)>=3( a²b²c²+ a²b²+a²c²+b²c²+a²+b+²c²+1)
<==> (a²+b²+c²)-(a²b²+a²c²+b²c²)-3 a²b²c²+3>=0
on suppose abc#0
si par exemple c=0 ==> ab=3 ==> 3+(a²+b²+c²)-(a²b²+a²c²+b²c²)-3 a²b²c²= a²+9/a²-6 =(a-3/a)²>=0.
Comme ab+bc+ac==3 ==> l'un des termes ab , bc et ac =<1 on suppose ab=<1 alors
(a²+b²+c²)-(a²b²+a²c²+b²c²)-3 a²b²c²+3>=0
<==> a²+b²-a²b² + (1-a²-b²-3a²b²) a²b² / (a+b)² +3>=0
<==> (a²+b²-a²b²)(a+b)² + a²b² (1-a²-b²-3a²b²) +3(a+b)²>=0
<==> (a²+b²-2a²b²+3)(a+b)² + a²b² (1+2ab-3a²b²) >=0
ce qui est vrai car
a²+b²-2a²b²+3>= 2ab-2a²b²+3=2ab( 1-ab)+3>=0
et 1+2ab-3a²b²=3ab(1-ab)>=0
| |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 16:39 Mar 21 Aoû 2012, 16:39 | |
| Mr Abdelbaki , vous pouvez ecrire cette partie en latex :
a²+b²-a²b² + (1-a²-b²-3a²b²) a²b² / (a+b)² +3>=0
<==> (a²+b²-a²b²)(a+b)² + a²b² (1-a²-b²-3a²b²) +3(a+b)²>=0
<==> (a²+b²-2a²b²+3)(a+b)² + a²b² (1+2ab-3a²b²) >=0
je n'arrive pas a bien vous suivre sur ce point , merci . | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 16:58 Mar 21 Aoû 2012, 16:58 | |
| - Oty a écrit:
- soit a,b,c >=0 tel que : ab+bc+ca=3 , Prouver que :
 . . On a: 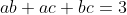 , donc on peut faire la substitution: \\&space;b=\sqrt{3}.\tan(\frac{\angle&space;B}{2})\\&space;c=\sqrt{3}.\tan(\frac{\angle&space;C}{2})&space;\end{matrix}\right.) tel que A, B et C sont les angles d'un triangle ABC. Et on a l'identité suivante: %20=%20\sqrt{\frac{(p-b)(p-c)}{p(p-a)}}\underset{\textrm{Ravi}}{=}\sqrt{\frac{xy}{z(x+y+z)}}) . Ainsi l'inégalité devient:  On remplace x, y et z par 1/x, 1/y et 1/z. Et il suffit montrer que:        Et on a:  , donc il suffit montrer que:  . Et d'après Schur:  , alors il suffit démontrer que:  ce qui est clairement vrai... CQFD. PS: Dans ma démo, j'ai considéré que les variables sont non-nuls , si l'un d'eux est égal à 0, l'inégalité se réduit à une avec un variable, ce qui est facilement démontrable. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 17:18 Mar 21 Aoû 2012, 17:18 | |
| BRAVO : Ali et Mr Abdelbaki  . | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 17:35 Mar 21 Aoû 2012, 17:35 | |
| Merci Oty  ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 18:54 Mar 21 Aoû 2012, 18:54 | |
| - Oty a écrit:
- soit a,b,c >=0 tel que : ab+bc+ca=3 , Prouver que :
 . . J'ai voulu rédiger cette solution vers midi, mais l'ordinateur s'est redémarré inopinément! Le même sort il y a quelques minutes... Mais, vu que personne n'a fait ce que j'ai en tête, je le partage encore une fois: Je distingue deux cas: *Si l'une des variables est nulle: On suppose par symétrie qu'on a c=0, la contrainte se réduit à ab=3, et on doit démontrer que  . Cette inégalité équivaut à 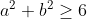 . Ce qui est trivialement vrai d'après l'inégalité arithmético-géométrique. *Si aucune des variables n'est nulle: On pose premièrement: 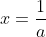 , 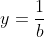 et 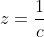 . Donc 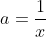 , 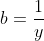 et 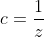 . La contrainte devient 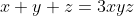 . Et l'inégalité, quant à elle, devient: 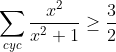 . On songe à l'inégalité de Jensen. On considère la fonction f définie par: =\frac{x^2}{x^2+1}) . La fonction f est dérivable sur l'ensemble des réels, et sa fonction dérivée:  ^2}) . La fonction f' est dérivable sur l'ensemble des réels, et on a: =\frac{2(1-x)^2}{(x^2+1)^3}) . Puisque f'' est positive ou nulle, on déduit que f est une fonction convexe. On peut donc appliquer l'inégalité de Jensen: \ge f(\sum_{cyc}\frac{1}{3}x})) . Soit ^2}{(\frac{x+y+z}{3})^2+1}=1-\frac{1}{(xyz)^2+1}) . ==>(1) D'un autre côté, on a selon l'inégalité arithmético-géométrique: ^{\frac{1}{3}}) . Ce qui veut bien dire que ^2\ge1) . Une simple manipulation nous emmène vers ^2+1}\ge\frac{1}{2}) . ==>(2) De 1 et 2, on conclut que 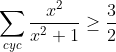 . *Les cas d'égalité: On déduit que notre inégalité devient une égalité si et seulement si: _Tous les variables valent 1 (Le second cas). _Une variable est nulle et les deux autres valent  . CQFD. Sauf erreurs.
Dernière édition par nmo le Mar 21 Aoû 2012, 19:01, édité 2 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 18:57 Mar 21 Aoû 2012, 18:57 | |
| @nmo jje n'arrive a voir que 4 formul de latex  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 18:58 Mar 21 Aoû 2012, 18:58 | |
| - Oty a écrit:
- @nmo jje n'arrive a voir que 4 formul de latex
 Je penses que c'est bon maintenant! Toutes les formules apparaissent! | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 | |
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mar 21 Aoû 2012, 19:11 Mar 21 Aoû 2012, 19:11 | |
| BRAVO : nmo  . Mr Abdelbaki j'ai vérifier votre solution Bravo comme deja dit  | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mer 22 Aoû 2012, 15:14 Mer 22 Aoû 2012, 15:14 | |
| une autre solution que j'ai trouvé :
l'un de ab et bc , ac est >= 1
donc on note 3 > x = ab >= 1( si ab = 3 donc c = 0 ce qui claire ...)
on utilisons la lemme : 1/(a²+1) + 1/(b²+1) >= 2/(x+1)
et on utilise aussi : x + c(a+b) = 3 donc
3 >= x+2sqrt(x)c donc c <= (3-x)(2sqrt(x))
et fainalement : 1/(c²+1) >= 4x/((3-x)² + 4x)
il suffit de montrer que : 2/(x+1) + 4x/((3-x)² + 4x) >= 1.5
ce qui est vrai parce que 3>x>=1 | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mer 22 Aoû 2012, 15:27 Mer 22 Aoû 2012, 15:27 | |
| derniere ineq equiv. a : ^2%20+%204x}%20-%201.5%20=%201.5\frac{(3-x)(x-1)^2}{(x+1)(x%C2%B2-2x+%209)}%20\geq%200) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  Mer 22 Aoû 2012, 15:32 Mer 22 Aoû 2012, 15:32 | |
| Bravp khay az360  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Inégalité (3) Sujet: Re: Inégalité (3)  | |
| |
|
  | |
| | Inégalité (3) |  |
|
