| | Topic des concours: |  |
|
+6ZYGOTO nmo judicecharatein amnay expert_run W.Elluizi 10 participants |
| Auteur | Message |
|---|
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Topic des concours: Sujet: Topic des concours:  Jeu 30 Aoû 2012, 13:05 Jeu 30 Aoû 2012, 13:05 | |
| Bonjour tout le monde,
Il va de soi que pour décrocher une bonne école,une bonne préparation s'impose.C'est dans cet esprit que j'ai pensé qu'on pourrait organiser un Topic pour traiter et les sujet d'oraux et les sujets d'écrit des concours.Je prie maintenant les intéressés de se manifester afin d'organiser et de commencer le topic. | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Ven 31 Aoû 2012, 13:06 Ven 31 Aoû 2012, 13:06 | |
| Etant donné qu'au moins un participant s'est manifeste ,nous pouvons commencer,mais en douceur avec cet oral de l'X qui est un peu un classique:
Montrer que l'ensemble P des nombres premiers est infini.montrer qu'il en est de meme pour les nombres premiers congrus à 3 modulo 4 | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Ven 31 Aoû 2012, 17:36 Ven 31 Aoû 2012, 17:36 | |
| Solution:
-------------------------------------------------------
On raisonne par l'absurde.
Supposons que l'ensemble P des premiers est fini avec P={P_1;P_2;...;P_n}.
Posons N=p_1.P_2....P_n+1
alors N n'admet aucun diviseur appartenant à P ce qui implique que N est premier.
D'où la contradiction puisque N n'appartient pas à P.
-------------------------------------------------------
Raisonnons encore par l'absurde:
Supposons que l'ensemble P des nombres premiers de forme 4k +3 est fini .
on pose P={P_1;P_2;..P_n} et N= 4 P_1.P_2...P_n-1=4(P_1.P_2...P_n-1)+3
N n'admet aucun diviseur premier appartenant à P
Alors soit N est premier soit il admet des diviseurs premiers de forme 4k+1.
Si N est premier alors c'est absurde puisque N n'appartient pas à P.
Si N admet des diviseurs premiers de forme 4k+1 alors lui aussi est de forme 4k+1 car (4k+1)(4z+1)=4(4kz+k+z)+1 ce qui est aussi absurde.
------------------------------------------------------
Soit n un entier naturel non nul et E_n l’équation : x^n. ln x = 1 d’inconnue x € R+*.
a) Montrer que l’équation E_n admet une unique solution x_n, et que x_n >= 1.
b) Montrer que la suite (x_n) est décroissante et converge vers 1.
| |
|
  | |
amnay
Débutant
 Nombre de messages : 1 Nombre de messages : 1
Age : 29
Date d'inscription : 31/08/2012
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Ven 31 Aoû 2012, 19:09 Ven 31 Aoû 2012, 19:09 | |
| 1/on pose fn(x)=x^n.ln(x)-1 et on applique TVI.
2/pour décroissante encore tvi, et pour la limite 1, on sait que Un converge et admet une limite l sup ou égale à 1. on suppose que l et sup strict à 1 on a alors limite de fn(x_n) différente de 1, contradiction car elle est constante en 1 donc l=1. | |
|
  | |
judicecharatein
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 30
Date d'inscription : 19/09/2011
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Sam 01 Sep 2012, 23:01 Sam 01 Sep 2012, 23:01 | |
| - amnay a écrit:
- 1/on pose fn(x)=x^n.ln(x)-1 et on applique TVI.
2/pour décroissante encore tvi, et pour la limite 1, on sait que Un converge et admet une limite l sup ou égale à 1. on suppose que l et sup strict à 1 on a alors limite de fn(x_n) différente de 1, contradiction car elle est constante en 1 donc l=1. euuuh ??! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Jeu 06 Sep 2012, 16:25 Jeu 06 Sep 2012, 16:25 | |
| - expert_run a écrit:
- Soit n un entier naturel non nul et E_n l’équation : x^n. ln x = 1 d’inconnue x € R+*.
a) Montrer que l’équation E_n admet une unique solution x_n, et que x_n >= 1.
b) Montrer que la suite (x_n) est décroissante et converge vers 1. Je crois que ce problème est classique, voici une solution: Soit n un entier naturel non nul. On définit la fonction réelle 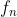 par: =1-x^n.\ln(x)) . a) La fonction 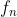 est dérivable (et continue par conséquent) sur 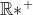 et on a :f_n'(x)=-\big(x^{n-1}(n.\ln(x)+1)\big)) . L'équation =0) conduit à +1=0) (car x est différent de 0) ou à =\frac{-1}{n}) ou bien à 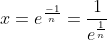 . On déduit que :f'(x)\le0) , donc 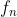 est strictement décroissante sur ] 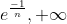 [ et a fortiori sur ] 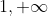 [. On sait de plus que =1) et =-\infty) , donc l'équation =0) admet une solution sur l'intervalle ] 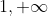 [. Cette solution est unique car la fonction 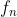 est bijective sur ] 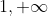 [ (elle est continue et strictement décroissante sur cet intervalle). On sait de plus que \ge f_n(x_n)=0) , ce qui conduit à 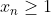 car 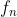 est décroissante. b) On a =0) , donc =1) . Et par suite =1-x_n^{n+1}.\ln(x_n)=1-x_n) en vertu de la dernière remarque. Or, on sait que 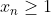 donc \le0=f_{n+1}(x_{n+1})) (l'équation ) admet une soltion unique 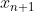 qui satisfait =0) ). Et puisque la fonction 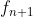 est strictement décroissante, on aura 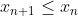 . La suite ) est ainsi décroissante. Et puisqu'elle est minorée par 1, elle est convergente. On appelle maintenant l la limite de notre suite, et calculons-la. On sait que =1) et =1) ce qui implique =x_{n+1}^{n+1}.ln(x_{n+1})) . En passant aux limites (en tendant n vers +l'infini) cela s'écrit: =l^{n+1}.ln(l)) . Cette équation admet comme solution 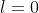 ou 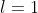 . Le cas 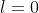 est exclus, par suite la suite ) converge vers 1. Sauf erreurs. | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Ven 14 Sep 2012, 20:40 Ven 14 Sep 2012, 20:40 | |
| - nmo a écrit:
- expert_run a écrit:
- Soit n un entier naturel non nul et E_n l’équation : x^n. ln x = 1 d’inconnue x € R+*.
a) Montrer que l’équation E_n admet une unique solution x_n, et que x_n >= 1.
b) Montrer que la suite (x_n) est décroissante et converge vers 1. Je crois que ce problème est classique, voici une solution:
Soit n un entier naturel non nul.
On définit la fonction réelle 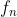 par: par: =1-x^n.\ln(x)) . .
a) La fonction 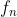 est dérivable (et continue par conséquent) sur est dérivable (et continue par conséquent) sur 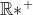 et on a et on a :f_n'(x)=-\big(x^{n-1}(n.\ln(x)+1)\big)) . .
L'équation =0) conduit à conduit à +1=0) (car x est différent de 0) ou à (car x est différent de 0) ou à =\frac{-1}{n}) ou bien à ou bien à 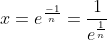 . .
On déduit que :f'(x)\le0) , donc , donc 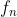 est strictement décroissante sur ] est strictement décroissante sur ]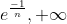 [ et a fortiori sur ] [ et a fortiori sur ]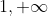 [. [.
On sait de plus que =1) et et =-\infty) , donc l'équation , donc l'équation =0) admet une solution sur l'intervalle ] admet une solution sur l'intervalle ]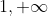 [. [.
Cette solution est unique car la fonction 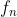 est bijective sur ] est bijective sur ]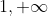 [ (elle est continue et strictement décroissante sur cet intervalle). [ (elle est continue et strictement décroissante sur cet intervalle).
On sait de plus que \ge f_n(x_n)=0) , ce qui conduit à , ce qui conduit à 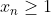 car car 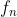 est décroissante. est décroissante.
b) On a =0) , donc , donc =1) . .
Et par suite =1-x_n^{n+1}.\ln(x_n)=1-x_n) en vertu de la dernière remarque. en vertu de la dernière remarque.
Or, on sait que 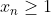 donc donc \le0=f_{n+1}(x_{n+1})) (l'équation (l'équation ) admet une soltion unique admet une soltion unique 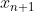 qui satisfait qui satisfait =0) ). ).
Et puisque la fonction 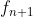 est strictement décroissante, on aura est strictement décroissante, on aura 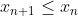 . .
La suite ) est ainsi décroissante. est ainsi décroissante.
Et puisqu'elle est minorée par 1, elle est convergente.
On appelle maintenant l la limite de notre suite, et calculons-la.
On sait que =1) et et =1) ce qui implique ce qui implique =x_{n+1}^{n+1}.ln(x_{n+1})) . .
En passant aux limites (en tendant n vers +l'infini) cela s'écrit: =l^{n+1}.ln(l)) . .
Cette équation admet comme solution 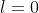 ou ou 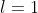 . .
Le cas 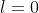 est exclus, par suite la suite est exclus, par suite la suite ) converge vers 1. converge vers 1.
Sauf erreurs. ça me parrait juste ,à toi nmo de proposer un problème. | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Jeu 04 Oct 2012, 22:29 Jeu 04 Oct 2012, 22:29 | |
| Vu que personne ne propose rien,je vous propose le problème suivant,tiré encore une fois d'un orale de l'X:
montrer que pour tout (m,n)£N²: ((2n!)*(2m!))/(m!*n!*((m+n)!))£N | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Lun 05 Nov 2012, 22:03 Lun 05 Nov 2012, 22:03 | |
| Bonsoir, je propose un nouveau problème ,beaucoup plus évident cette fois ci ,avec l'espoir qu'il y aura plus de participation: Montrer l'existence et l'unicité des suites _{n\in \mathbb{N}}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?(a_{n})_{n\in \mathbb{N}}" title="(a_{n})_{n\in \mathbb{N}}" /></a>) et _{n\in \mathbb{N}}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?(b_{n})_{n\in \mathbb{N}}" title="(b_{n})_{n\in \mathbb{N}}" /></a>) telles que : ^{n}=a_{n}@plus;b_{n}\sqrt{2}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\forall n\in \mathbb{N}: (\sqrt{2}+1)^{n}=a_{n}+b_{n}\sqrt{2}" title="\forall n\in \mathbb{N}: (\sqrt{2}+1)^{n}=a_{n}+b_{n}\sqrt{2}" /></a>) et montrer que: (\exists !p\in \mathbb{N}): (\sqrt{2}@plus;1)^{n}=\sqrt{p}@plus;\sqrt{p-1}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?(\forall n\in \mathbb{N})(\exists !p\in \mathbb{N}): (\sqrt{2}+1)^{n}=\sqrt{p}+\sqrt{p-1}" title="(\forall n\in \mathbb{N})(\exists !p\in \mathbb{N}): (\sqrt{2}+1)^{n}=\sqrt{p}+\sqrt{p-1}" /></a>) | |
|
  | |
ZYGOTO
Féru
 Nombre de messages : 58 Nombre de messages : 58
Age : 31
Date d'inscription : 19/10/2011
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Sam 17 Nov 2012, 01:15 Sam 17 Nov 2012, 01:15 | |
|
Dernière édition par ZYGOTO le Sam 17 Nov 2012, 13:30, édité 1 fois | |
|
  | |
ZYGOTO
Féru
 Nombre de messages : 58 Nombre de messages : 58
Age : 31
Date d'inscription : 19/10/2011
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Sam 17 Nov 2012, 01:20 Sam 17 Nov 2012, 01:20 | |
| oral X:
Soit E un ensemble. Montrer que E est infini si, et seulement si, pour toute fonction f:E→E, il existe A⊂E avec A≠∅ et A≠E telle que f(A)⊂A. | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Sam 17 Nov 2012, 09:58 Sam 17 Nov 2012, 09:58 | |
| - nmo a écrit:
- expert_run a écrit:
- Soit n un entier naturel non nul et E_n l’équation : x^n. ln x = 1 d’inconnue x € R+*.
a) Montrer que l’équation E_n admet une unique solution x_n, et que x_n >= 1.
b) Montrer que la suite (x_n) est décroissante et converge vers 1. Je crois que ce problème est classique, voici une solution:
Soit n un entier naturel non nul.
On définit la fonction réelle 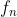 par: par: =1-x^n.\ln(x)) . .
a) La fonction 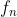 est dérivable (et continue par conséquent) sur est dérivable (et continue par conséquent) sur 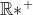 et on a et on a :f_n'(x)=-\big(x^{n-1}(n.\ln(x)+1)\big)) . .
L'équation =0) conduit à conduit à +1=0) (car x est différent de 0) ou à (car x est différent de 0) ou à =\frac{-1}{n}) ou bien à ou bien à 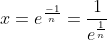 . .
On déduit que :f'(x)\le0) , donc , donc 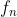 est strictement décroissante sur ] est strictement décroissante sur ]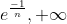 [ et a fortiori sur ] [ et a fortiori sur ]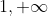 [. [.
On sait de plus que =1) et et =-\infty) , donc l'équation , donc l'équation =0) admet une solution sur l'intervalle ] admet une solution sur l'intervalle ]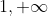 [. [.
Cette solution est unique car la fonction 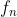 est bijective sur ] est bijective sur ]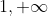 [ (elle est continue et strictement décroissante sur cet intervalle). [ (elle est continue et strictement décroissante sur cet intervalle).
On sait de plus que \ge f_n(x_n)=0) , ce qui conduit à , ce qui conduit à 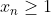 car car 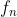 est décroissante. est décroissante.
b) On a =0) , donc , donc =1) . .
Et par suite =1-x_n^{n+1}.\ln(x_n)=1-x_n) en vertu de la dernière remarque. en vertu de la dernière remarque.
Or, on sait que 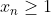 donc donc \le0=f_{n+1}(x_{n+1})) (l'équation (l'équation ) admet une soltion unique admet une soltion unique 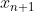 qui satisfait qui satisfait =0) ). ).
Et puisque la fonction 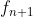 est strictement décroissante, on aura est strictement décroissante, on aura 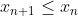 . .
La suite ) est ainsi décroissante. est ainsi décroissante.
Et puisqu'elle est minorée par 1, elle est convergente.
On appelle maintenant l la limite de notre suite, et calculons-la.
On sait que =1) et et =1) ce qui implique ce qui implique =x_{n+1}^{n+1}.ln(x_{n+1})) . .
En passant aux limites (en tendant n vers +l'infini) cela s'écrit: =l^{n+1}.ln(l)</font>) . .
Cette équation admet comme solution 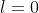 ou ou 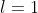 . .
Le cas 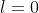 est exclus, par suite la suite est exclus, par suite la suite ) converge vers 1. converge vers 1.
Sauf erreurs. ce qui est rouge est faux, n-->+oo partout x_n>1 ==> l>=1 x_n^n ln(x_n)=1===> nln(x_n)+ln(ln(x_n))=0 on pose y_n=ln(x_n) ==> y_n>0 et ln(y_n)/y_n=-n--->-oo ==> l=1 car sinon y_n---> ln(l)>0 ==> ln(y_n)/y_n--->ln(ln(1))/ln(l) Question
trouver un équivalent simple de x_n-1 | |
|
  | |
Vz
Féru

 Nombre de messages : 63 Nombre de messages : 63
Age : 31
Date d'inscription : 14/11/2010
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Sam 17 Nov 2012, 11:58 Sam 17 Nov 2012, 11:58 | |
| | |
|
  | |
Saiichi
Féru

 Nombre de messages : 30 Nombre de messages : 30
Age : 30
Localisation : marrakech
Date d'inscription : 26/10/2012
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Jeu 27 Déc 2012, 14:28 Jeu 27 Déc 2012, 14:28 | |
| ok je veux participer avec vous | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  Ven 28 Déc 2012, 13:01 Ven 28 Déc 2012, 13:01 | |
| - W.Elluizi a écrit:
- Vu que personne ne propose rien,je vous propose le problème suivant,tiré encore une fois d'un orale de l'X:
montrer que pour tout (m,n)£N²: ((2n!)*(2m!))/(m!*n!*((m+n)!))£N Cet exercice se résout facilement avec la formule de Legendre en montrant l'inégalité classique E(2m)+E(2n)>=E(m)+E(n)+E(m+n) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Topic des concours: Sujet: Re: Topic des concours:  | |
| |
|
  | |
| | Topic des concours: |  |
|
