x+y+z<=xyz

soient x,y,z appartient a ]-1;1[ tq $x+y+z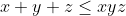<=xyz Gif$ MQ:

$x+y+z<=xyz Gif$

Sujet: Re: x+y+z<=xyz Sam 01 Sep 2012, 14:54

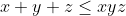younesmath2012 a écrit:: soient x,y,z appartient a ]-1;1[ tq $x+y+z<=xyz Gif$ MQ:
$x+y+z<=xyz Gif$

Voici ma solution:
On se contente de poser 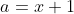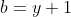$x+y+z<=xyz Gif$ , $x+y+z<=xyz Gif$ et 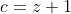$x+y+z<=xyz Gif$ .
Les réels a, b et c appartiennent à l'intervalle ] 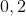$x+y+z<=xyz Gif$ [.
La condition devient 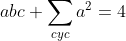$x+y+z<=xyz Gif$ .
Et l'inégalité s'écrit 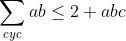$x+y+z<=xyz Gif$ .
On analyse maintenant la nouvelle condition de plus près; si on divise les deux côtés par 4, on trouve que $x+y+z<=xyz Gif$ .
On pose alors 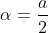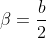$x+y+z<=xyz Gif$ , $x+y+z<=xyz Gif$ et 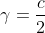$x+y+z<=xyz Gif$ .
Il vient que 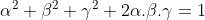$x+y+z<=xyz Gif.latex?\alpha^2+\beta^2+\gamma^2+2\alpha.\beta$ et les réels 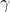$x+y+z<=xyz Gif$ , $x+y+z<=xyz Gif$ et $x+y+z<=xyz Gif$ appartiennent à l'intervalle ] 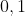$x+y+z<=xyz Gif$ [.
Et on doit donc démontrer que 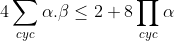$x+y+z<=xyz Gif.latex?4\sum_{cyc}\alpha$ , soit en réduisant 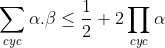$x+y+z<=xyz Gif.latex?\sum_{cyc}\alpha$ .
Et ici la condition et l'inégalité devient moins féroce.
Sauf erreurs.
P.S: Je continue mes remarques dans mon prochain message.

Sujet: Re: x+y+z<=xyz Sam 01 Sep 2012, 15:10

Pour compléter ce que je viens de poster, il faut assurément se rendre compte que l'exercice courant est très connu et il suffit de chercher la solution quelque part.
Pour moi, je vous propose ce sujet où se trouve une très bonne approche du problème: https://mathsmaroc.jeun.fr/t17337-nice.
Et pour l'inégalité de Walker, il faut lire un document téléchargeable depuis le lien suivant http://www.fichier-pdf.fr/2010/12/03/geo-triangle/.
Au plaisir!
P.S: Je me demande s'il y aurait des solutions sans approches géométrique; ils sont les bienvenus!

Sujet: Re: x+y+z<=xyz Sam 01 Sep 2012, 15:39

oki dear nmo voila ce que je fais :
on a : a²+b²+c²+abc = 4 et on doit prouver que : ab+bc+ca <= 2 + abc
on peut supposer que : c(a-1)(b-1) >= 0 donc : abc + c >= ac + bc alors : abc + 2 >= ac+bc + 2 -c
alors il suffit de montrer que : c + ab <= 2
on pose x = ab
on a :
4 = a²+b²+c²+abc >= 2x + c² + xc = x(c+2) + c²
et donc : x <= (4-c²)/c+2 = 2-c
donc : x+c <= 2-c+c = 2 d'ou le resultat !!