Exos faciles

Sujet: Exos faciles Mer 10 Oct 2012, 18:55

Voici deux petits exercices faciles :
Montrer que pour tout 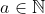$Exos faciles Gif$ :
1) 3a-1 n'est pas un carré parfait
2) a s'écrit sous la forme : $Exos faciles Gif$

Sujet: Re: Exos faciles Dim 14 Oct 2012, 13:22

1) Supposons par absurde que 3a-1=n² / n appartient à IN.
Et donc 3a=n²+1

Et donc (n²+1)/3=a

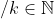on a : On a n appartient à IN , donc: $Exos faciles Gif$ $Exos faciles K\in&space;\mathbb{N}$

$Exos faciles Gif$

On étudie les cas :
1er cas: n²=9k²
Alors: $Exos faciles Gif$

2ème cas:n²=9k²+6k+1

Donc: $Exos faciles Gif.latex?\frac{n^{2}+1}{3}=\frac{9k^{2}+6k+1+1}{3}=\frac{3(k^{2}+k)+2}{3}=k^{2}+k+\frac{2}{3}$

3ème cas: n²=9k²+12k+4

Et donc: $Exos faciles Gif$

Donc : $Exos faciles Gif.latex?\forall&space;n\in&space;\mathbb{N}:\frac{n^{2}+1}{3}\notin&space;\mathbb{N}$

On en déduit que : n²+1#3a
Et donc 3a-1 n'est pas un carré parfait.

2) Prouvons que a=2^q(2p+1)

On a

$Exos faciles &space;(k,p)\in&space;\mathbb{N}^{2}$

k appartient à IN <=> k est pair ou k est impair.
Et donc : $Exos faciles &space;(n,p,r)\in&space;\mathbb{N}^{3}$

Et donc: $Exos faciles &space;(p,q)\in&space;\mathbb{N}^{2}$

Sujet: Re: Exos faciles Dim 14 Oct 2012, 13:23

P.S: L'exercice 1 est déjà posté dans un aure topic.

Sujet: Re: Exos faciles Sam 20 Oct 2012, 13:29

Soukaina Amaadour , j'ai pas bien compris ta solution du 2eme exo , tu peux mieux expliquer ? Smile

Sujet: Re: Exos faciles Sam 20 Oct 2012, 22:29

Gauss-Maxwell a écrit:: Soukaina Amaadour , j'ai pas bien compris ta solution du 2eme exo , tu peux mieux expliquer ?

Si a est impair, alors il s'écrit sous la forme suivante: a=2p+1

Si a est pair, alors il s'écrit de la façon suivante: a=2k / k appartient à IN

*Si K est impair alors a=2^1 *(2r+1)

*Si k est pair alors : a=2^2*k'
.......

Alors d'une façon générale : tout entier s'ecrit sous la forme : a=2^q *(2p+1) /(p,q) apprtiennent à IN²

Sujet: Re: Exos faciles Mer 24 Oct 2012, 23:51

Soukaina Amaadour a écrit:

Gauss-Maxwell a écrit:: Soukaina Amaadour , j'ai pas bien compris ta solution du 2eme exo , tu peux mieux expliquer ?

Si a est impair, alors il s'écrit sous la forme suivante: a=2p+1
Si a est pair, alors il s'écrit de la façon suivante: a=2k / k appartient à IN
*Si K est impair alors a=2^1 *(2r+1)
*Si k est pair alors : a=2^2*k'
......
Alors d'une façon générale : tout entier s'ecrit sous la forme : a=2^q *(2p+1) /(p,q) apprtiennent à IN²

Il faut chercher une démonstration de ce que tu dis, en d'autre terme: c'est quoi q par rapport à l'entier a?
Je te laisse réfléchir encore une fois.

Sujet: Re: Exos faciles Jeu 25 Oct 2012, 10:37

2) n doit être non nul
q=Max{m dans N: 2^m divise n}

Sujet: Re: Exos faciles Sam 27 Oct 2012, 17:59

abdelbaki.attioui a écrit:: 2) n doit être non nul
q=Max{m dans N: 2^m divise n}

Oui, c'est la bonne réponse.
Il suffit de faire la décomposition de n en facteurs premiers.
On aura: 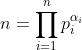$Exos faciles Gif$ où les 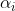$Exos faciles Gif$ sont des entiers naturels, les 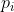$Exos faciles Gif$ sont des entiers premiers.
Ce qui deviendra encore: 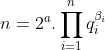$Exos faciles Gif.latex?n=2^a$ avec les 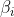$Exos faciles Gif$ sont des entiers naturels, les 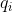$Exos faciles Gif$ sont des entiers premiers tous différent de 2.
Il s'ensuit que 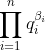$Exos faciles Gif$ est un entier impair.
On pose 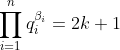$Exos faciles Gif$ tel que k est un entier naturel.
Finalement, on aura $Exos faciles Gif.latex?(\forall n\in\mathhbb{N}) : (\exists (a,k)\in\mathbb{N}^2) :n=2^a$ .
Sauf erreurs.

» EXOS lim
» faciles mais belles !!
» exos lim!
» Exos Lim
» exo des exos!!!