de vasile cirtoage 2006

Sujet: de vasile cirtoage 2006 Dim 21 Oct 2012, 18:48

a,b,c >=0 tq a+b+c=3 montrer que : 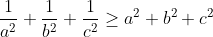$de vasile cirtoage 2006 Gif$

Sujet: Re: de vasile cirtoage 2006 Dim 28 Oct 2012, 02:14

Salut,

$de vasile cirtoage 2006 Gif$

Sujet: Re: de vasile cirtoage 2006 Dim 28 Oct 2012, 11:48

Humber a écrit:: Salut,

$\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\geq\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac} \\ \newline \text{Il suffit donc de montrer que :}\\ \left (\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\geq a^2+b^2+c^2 \right) \Leftrightarrow \left (\frac{3}{abc}\geq a^2+b^2+c^2 \right ) \\ \newline~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\Leftrightarrow \fbox{abc( a^2+b^2+c^2)\leq3}~~ \fbox{1} \newline \\ \text{D'après l'inégalité :} (ab+bc+ac)^2\geq <font color=$ abc(a+b+c)%20~~\text{On%20a%20:%20}\fbox{abc%20\leq%20\frac{(ab+bc+ac)^2}{3}}%20~~\fbox{2}%20\newline%20\newline%20\text{Enfin,%20on%20sait%20bien%20que%20:%20}(a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ac)%20\\\\%20~~~~~~~~~~~~~~~~~~~~~~~~~~~~\Leftrightarrow%20~\fbox{(a^2+b^2+c^2)=\left%209-2(ab+bc+ac)}~~\fbox{3}%20\\\\\text{Avec%202%20et%203%20:%20}%20\fbox{1}\Leftrightarrow\frac{(ab+bc+ac)^2}{3}(9-2(ab+bc+ac))\leq3~~%20\\%20~~~~~~~~~~~~~~~~~~~~~~\Leftrightarrow%20\frac{p^2}{3}(9-2p)\leq3~~~\text{O%C3%B9%20p=ab+bc+ac}%20\\%20~~~~~~~~~~~~~~~~~~~~~~%20\Leftrightarrow-(p-3)^2(2p+3)\leq0%20~~~~\text{Vrai%20!}" border="0" alt=""/>

votre methode est simple et jolie Mr "Humber" mais vous avez commis une!!! petite erreure !!! on ne peut pas avoir votre derniere ligne sauf si vous remplacer ce qui est en rouge par 3abc(a+b+c)
ce 3 vous manque dans les autres lignes jusqu'a la fin

Sujet: Re: de vasile cirtoage 2006 Dim 28 Oct 2012, 13:20

younesmath2012 a écrit:

Humber a écrit:: Salut,

$\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\geq\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac} \\ \newline \text{Il suffit donc de montrer que :}\\ \left (\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\geq a^2+b^2+c^2 \right) \Leftrightarrow \left (\frac{3}{abc}\geq a^2+b^2+c^2 \right ) \\ \newline~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\Leftrightarrow \fbox{abc( a^2+b^2+c^2)\leq3}~~ \fbox{1} \newline \\ \text{D'après l'inégalité :} (ab+bc+ac)^2\geq <font color=$ abc(a+b+c)%20~~\text{On%20a%20:%20}\fbox{abc%20\leq%20\frac{(ab+bc+ac)^2}{3}}%20~~\fbox{2}%20\newline%20\newline%20\text{Enfin,%20on%20sait%20bien%20que%20:%20}(a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ac)%20\\\\%20~~~~~~~~~~~~~~~~~~~~~~~~~~~~\Leftrightarrow%20~\fbox{(a^2+b^2+c^2)=\left%209-2(ab+bc+ac)}~~\fbox{3}%20\\\\\text{Avec%202%20et%203%20:%20}%20\fbox{1}\Leftrightarrow\frac{(ab+bc+ac)^2}{3}(9-2(ab+bc+ac))\leq3~~%20\\%20~~~~~~~~~~~~~~~~~~~~~~\Leftrightarrow%20\frac{p^2}{3}(9-2p)\leq3~~~\text{O%C3%B9%20p=ab+bc+ac}%20\\%20~~~~~~~~~~~~~~~~~~~~~~%20\Leftrightarrow-(p-3)^2(2p+3)\leq0%20~~~~\text{Vrai%20!}" border="0" alt=""/>

votre methode est simple et jolie Mr "Humber" mais vous avez commis une!!! petite erreure !!! on ne peut pas avoir votre derniere ligne sauf si vous remplacer ce qui est en rouge par 3abc(a+b+c)
ce 3 vous manque dans les autres lignes jusqu'a la fin

Je te remercie pour ta remarque Younes, C'est corrigé ^^

Sujet: Re: de vasile cirtoage 2006 Dim 28 Oct 2012, 13:20

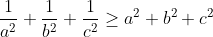younesmath2012 a écrit:: a,b,c >=0 tq a+b+c=3 montrer que : $de vasile cirtoage 2006 Gif$

Ma solution : l'inégalité est equivalente a :
$de vasile cirtoage 2006 Gif$
cette derniere est vrai due a deux inégalité tres connue :
$de vasile cirtoage 2006 Gif$
Fin de la démonstration !

Sujet: Re: de vasile cirtoage 2006 Dim 28 Oct 2012, 14:48

Pourrais tu montrer comment tu as trouvé la première ligne de ta démo ?

Sujet: Re: de vasile cirtoage 2006 Dim 28 Oct 2012, 15:00

Humber a écrit:: Pourrais tu montrer comment tu as trouvé la première ligne de ta démo ?

on a a+b+c=3 , donc (a+b+c)^5 = 81(a+b+c)=243 et on multiplit l'inégalité par ce nombre

Sujet: Re: de vasile cirtoage 2006 Dim 28 Oct 2012, 15:22

Oty a écrit:

Humber a écrit:: Pourrais tu montrer comment tu as trouvé la première ligne de ta démo ?

on a a+b+c=3 , donc (a+b+c)^5 = 81(a+b+c)=243 et on multiplit l'inégalité par ce nombre

$de vasile cirtoage 2006 Gif.latex?\text{Si%20on%20fait%20ce%20que%20tu%20dis%20:%20}\\%20\text{L'in%C3%A9galit%C3%A9%20de%20d%C3%A9part%20:%20}\Leftrightarrow%20\sum%20a^2b^2\geq%20a^2b^2c^2(a^2+b^2+c^2)%20\\%20~~~~~\text{En%20multipliant%20par%20}(a+b+c)^5%20~~\text{On%20a%20:%20}\\%20(a+b+c)^5\sum%20a^2b^2%20\geq%2081.a^2b^2c^2(a^2+b^2+c^2)(a+b+c)%20\\%20\\%20\text{Et%20d'apr%C3%A8s%20toi%20}81$

Sujet: v Dim 28 Oct 2012, 17:37

Oty a écrit:

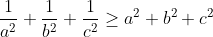
younesmath2012 a écrit:: a,b,c >=0 tq a+b+c=3 montrer que : $de vasile cirtoage 2006 Gif$

Ma solution : l'inégalité est equivalente a :
$de vasile cirtoage 2006 Gif$
cette derniere est vrai due a deux inégalité tres connue :
$de vasile cirtoage 2006 Gif$
Fin de la démonstration !

Bravo Mr ''oty'' mais vous avez utilisé une inegalite ''etrangere'' du docteur Mr'' vasile cirtoage''
pour l'utiliser il faut d'abord la demontrer
vous avez aussi fait une faute de frappe vous avez ecrit $de vasile cirtoage 2006 Gif$ au lieu de $de vasile cirtoage 2006 Gif$
donc la reponse de Mr ''Humber'' me semble la plus simple et la plus belle!!! (excusez moi)!!!

Sujet: Re: de vasile cirtoage 2006 Dim 28 Oct 2012, 17:59

Oui c'est réctifier Mr Younes , pour moi aussi la solution de Mr Humber me semble bien Meilleur que la mienne .

Sujet: Re: de vasile cirtoage 2006 Lun 29 Oct 2012, 21:51

Salam,

Je pense que l'idée de l'exo est:

(ab+bc+ac)²(a²+b²+c²)=(ab+bc+ac)²((a+b+c)²-2(ab+bc+ac))<=((a+b+c)²/3)^3 par AM-GM

» de vasile cirtoage 2005
» de vasile cirtoage 2001
» de vasile cirtoage 2005.
» de vasile cirtoage 2005!
» Vasile Cirtoaje