| | Combinatoire et arithmetique |  |
|
|
| Auteur | Message |
|---|
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Combinatoire et arithmetique Sujet: Combinatoire et arithmetique  Ven 12 Avr 2013, 20:53 Ven 12 Avr 2013, 20:53 | |
| Qu'elle est la probabilite que en prenant 2 nombre ils soient premiers entre eux ? Bon corage a tous  | |
|
  | |
mt2sr
Maître

 Nombre de messages : 104 Nombre de messages : 104
Date d'inscription : 16/01/2006
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Ven 12 Avr 2013, 22:03 Ven 12 Avr 2013, 22:03 | |
| c'est 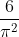 | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Sam 13 Avr 2013, 09:40 Sam 13 Avr 2013, 09:40 | |
| Exact  tu le prouve avec des convulution ou pas? | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Sam 13 Avr 2013, 10:13 Sam 13 Avr 2013, 10:13 | |
| BJR au Forum !! @ galillee56 Tu pourrais jeter un Coup d'Oeil ICI https://mathsmaroc.jeun.fr/t20176-endomorphismes-de-l-anneau-c#168889Ce serait très enrichissant pour Toi ... D'autre part , Je ne vois pas ce que vient faire l'opération de Convolution , dans cette question qui a une coloration Probabiliste ??!! Ce serait mieux si vous pouvez Modéliser le Problème convenablement , ce serait intéressant pour tout le monde .... Vive le Partage . Amicalement . LHASSANE | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Sam 13 Avr 2013, 11:58 Sam 13 Avr 2013, 11:58 | |
| Bjr M Oeil de lynx
en fait les convolution en arithmetique sont un peu differente des covolution en analyse (mais trop quand meme voir: http://fr.wikipedia.org/wiki/Convolution_de_Dirichlet)
mnt phi(n) (la fonction indicatrice d'euler vaut) ph=u*id u:etant la fonction de mobius (http://fr.wikipedia.org/wiki/Fonction_de_M%C3%B6bius) maintenant retournons a l'exo le nombre de nombre de nombre premier avec un certain k est phi(k) donc ma probablite vaut (somme(phi(k) k:=1..n)/(2 parmi n) et on calcule avec des convolution ca donne la somme des u(d)/d^2 et ca tend vers PI^2/6 ca cetait la preuve que j ai faite mais MR mt2sr a surement une preuve moin complique | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Sam 13 Avr 2013, 21:18 Sam 13 Avr 2013, 21:18 | |
| BSR galillee56
Pour Moi , cette méthode permet de calculer la limite quand n -----> +oo de
l'expression(1/n^2). Card { (u,v) dans IN*xN* ; 1=< u,v =<n avec PGCD(u;v)=1}
Je voudrais bien connaitre une Approche PROBABILISTE du Problème et un Passage du cas Discret fini à " n ----> +oo "
Je suis Pédagogue et Ancien Prof. de Fac , à la Retraite actuellement et comme tous les Enseignants , Je suis Partisan de la Rigueur ....
Amicalement . LHASSANE | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Dim 14 Avr 2013, 11:16 Dim 14 Avr 2013, 11:16 | |
| bonjour mr oeil de lynx alors j'ai essaye de bien rediger pour me faire comprendre et j'espere que ca sera bon
alors on sait que le nombre de nombre premier avec k est phi(k) maintenant retreignons notre travail a [1,n] le nombre de nombre premier avec n est phi(n) avec n-1 est phi(n-1)... le nombre de couple (k,x) tel que x soit premier avec k est phi(k) donc sur [1,n] le nombre de nombre premier entre est sum(phi(k),k=1...n) donc la probabilite sur [1,n] de prendre de nombre entiers et qui soit premier entre eux est Pn=(sum(phi(k),k=1...n))/n^2 maintenant pour calculer la somme des phi(k) on utilise les convolution de dirichlet phi=u*id donc sum(phi(k),k=1...n)=sum(u*id(k),k=1..n) on a f*g=somme(f(d)g(n/d),d divisant n) donc on faisant un petit de variable sur les bord on trouve que sum(f*g)=sum(f(d),d<=x)sum(g(k),k<=x/d) donc (sum(phi(k),k=1...n)=sum(u(d),d<=n)sum(id(k),k<=n/d) donc (sum(phi(k),k=1...n)= sum(u(d)[n/d]([n/d]+1),d<=n) on remplace cette expression dans Pn maintenant Pn c'est la probabilite sur l'intervalle [1,n] pour avoir le resultat sur N on fait tendre n vers + linf ce qu il faut savoir c est que som(u(d)/d^2,d<n) tend vers 6/(pi^2) et la som(u(d)/d,d<n) est borne donc la probablite est de 6/pi^2
Dernière édition par galillee56 le Dim 14 Avr 2013, 11:32, édité 1 fois | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Dim 14 Avr 2013, 11:18 Dim 14 Avr 2013, 11:18 | |
| il y a surement une preuve plus facile que celle ci mais celle ci me parait evidente si on maitrise les convolution | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Dim 14 Avr 2013, 13:30 Dim 14 Avr 2013, 13:30 | |
| BJR galillee56
Ce n'est pas tant Ta Démonstration qui me cause des Soucis ...
Mais plutôt la Démarche .
Je te file un Lien assez Intéressant ou il est Question d'une Vieille Démo dûe à EULER .
Suis le Fil du Topic ICI , c'est très Enrichissant ....
http://www.maths-forum.com/proba-2-nombres-soient-premier-entre-eux-86014.php
Amicalement . LHASSANE | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Dim 14 Avr 2013, 13:37 Dim 14 Avr 2013, 13:37 | |
| Pourquoi ma demarche est fausse j'arrive pas a comprendre? | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Dim 14 Avr 2013, 13:46 Dim 14 Avr 2013, 13:46 | |
| Je n'ai jamais dit que la Démo était fausse galilllee56 !!
C'est la manière d'entrevoir la Question ...
La Modélisation Probabiliste etc ....
Mais , J'ai parfaitement Compris Ta Démo ... avec la Convolution etc ... | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  Dim 14 Avr 2013, 14:12 Dim 14 Avr 2013, 14:12 | |
| C vrai que on pouvait faire plus simple c juste que je suis habitue a calculer des convolution mais je comprend toit a fait votre remarque et je vois remercie pour vos remarque pertinente  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Combinatoire et arithmetique Sujet: Re: Combinatoire et arithmetique  | |
| |
|
  | |
| | Combinatoire et arithmetique |  |
|
