- hilbert_1988 a écrit:
- Salut tout le monde,
Je vous propose cette jolie inégalité.
Soit n un entier naturel supérieur à 1 et x un réel. Montrer que :
Je propose ma solution par récurrence sur l'entier n:
*Initialisation:
Pour
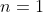
, on est amené à prouver que:
+\sin^{6}(x)\le\cos^2(2x)+\frac{\sin^2(2x)}{4})
.
Cette inégalité s'écrit:
+\sin^{6}(x)+3\cos^2(x).\sin^2(x)(\cos^2(x)+\sin^2(x))\le(\cos^2(x)-\sin^2(x))^2+4\cos^2(x).\sin^2(x))
.
Soit encore:
+\sin^2(x))^3\le(\cos^2(x)+\sin^2(x))^2)
.
Ce qui est clairement vrai car l'inégalité est réduite à une égalité.
*Hérédité:
Supposons que la propriété est vraie pour un certain entier n, c'est à dire que:
+\sin^{2n+4}(x)\le\cos^2(2x)+\frac{\sin^2(2x)}{2^{n+1}})
.
Et montrons qu'elle est vraie pour son succeur n+1, c'est à dire que:
+\sin^{2n+6}(x)\le\cos^2(2x)+\frac{\sin^2(2x)}{2^{n+2}})
.
On a:
+\sin^{2n+4}(x)\le\cos^2(2x)+\frac{\sin^2(2x)}{2^{n+1}})
.
Donc:
+\sin^2(x)).(\cos^{2n+4}(x)+\sin^{2n+4}(x))\le\cos^2(2x)+\frac{\sin^2(2x)}{2^{n+1}})
.
Et ainsi:
+\sin^{2n+6}(x)\le\cos^2(2x)+\frac{\sin^2(2x)}{2^{n+1}}-\cos^2(x).\sin^2(x).(\sin^{2n+2}(x)+\cos^{2n+2}(x)))
.
Il suffit donc de prouver que:
+\frac{\sin^2(2x)}{2^{n+1}}-\cos^2(x).\sin^2(x).(\sin^{2n+2}(x)+\cos^{2n+2}(x))\le\cos^2(2x)+\frac{\sin^2(2x)}{2^{n+2}})
ou encore:
}{2^{n+1}}\le\cos^2(x).\sin^2(x).(\sin^{2n+2}(x)+\cos^{2n+2}(x))+\frac{\sin^2(2x)}{2^{n+2}})
.
Cette dernière inégalité s'écrit:
.\cos^2(x)}{2^{n-1}}\le\cos^2(x).\sin^2(x).(\sin^{2n+2}(x)+\cos^{2n+2}(x))+\frac{\sin^2(x).\cos^2(x)}{2^n})
soit:
.\cos^2(x)\le2^n.\cos^2(x).\sin^2(x).(\sin^{2n+2}(x)+\cos^{2n+2}(x)))
.==>(*)
Il est évident que la fonction
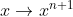
est convexe.
Il vient donc que:
+\cos^2(x))\bigg)^{n+1}\le\frac{1}{2}.(\sin^2(x))^{n+1}+\frac{1}{2}.(\cos^2(x))^{n+1})
.
Soit:
)^{n+1}+(\cos^2(x))^{n+1}\bigg))
.
Il s'ensuit donc que * est vraie, d'où le résultat.
*Conclusion de la récurrence:
On a:
: \cos^{2n+4}(x)+\sin^{2n+4}(x)\le\cos^2(2x)+\frac{\sin^2(2x)}{2^{n+1}})
.
CQFD.
Sauf erreurs.
