| | suite réelle |  |
|
|
| Auteur | Message |
|---|
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: suite réelle Sujet: suite réelle  Mer 30 Oct 2013, 21:59 Mer 30 Oct 2013, 21:59 | |
| Bonjour
Soit $ (a_n)$ et $ (b_n)$ deux suites à termes positifs telles que $ \lim (a_n)^n = a >0$ et $ \lim(b_n)^n = b > 0 $ et $ p, q$ deux réels $ > 0$ tels que $ p+q = 1$.
Quelle est la nature de la suite $ (p.a_n +q.b_n)^n$.
J'ai démontré que $ \lim a_n = 1$ et $ \lim b_n = 1$ | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  Jeu 31 Oct 2013, 10:29 Jeu 31 Oct 2013, 10:29 | |
| a_n-->a>0 et b_n-->b>0 ==> les suites (a_n) et (b_n) sont >0 à partir d'un certain rang.
On peut alors supposer que u(n)=(p.a_n +q.b_n)^n>0
p.a_n +q.b_n -->pa+qb>0
si pa+qb>1==> u(n)-->+00
si pa+qb<1==> u(n)-->0
si pa+qb=1, on ne peut rien dire.
Pour a_n=b_n=1+1/n^s ==> a=b=1 , qqs p,q>0 : p+q=1 , ( s>0 à choisir après)
u(n)=(1+1/n^s)^n
ln(u(n))=n ln( 1+1/n^s) ~ n^(1-s)
pour s=1, u(n) --> e
pour 0<s<1, u(n) --> +00
pour s>1, u(n) --> 1 | |
|
  | |
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  Jeu 31 Oct 2013, 12:14 Jeu 31 Oct 2013, 12:14 | |
| p.a_n + q.b_n n'est pas constant
de plus
p.a_n + q.b_n tend vers 1 car a_n tend vers 1 de même pour b_n
amicalement | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  Jeu 31 Oct 2013, 20:38 Jeu 31 Oct 2013, 20:38 | |
| Je pense que ma solution est complète et mal comprise ( sauf erreur)
je ne vois pas pourquoi a_n tend vers 1 de même pour b_n
Exemples : p,q>0 : p+q=1
1) a_n=b_n=1 ==> p.a_n + q.b_n=1
2) a_n=b_n=1/2 ==> (p.a_n + q.b_n)^n=1/2^n --->0
2) a_n=b_n=2 ==> (p.a_n + q.b_n)^n= 2^n --->+00 | |
|
  | |
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  Jeu 31 Oct 2013, 21:39 Jeu 31 Oct 2013, 21:39 | |
| lim (a_n)^n = a >0 et lim(b_n)^n = b > 0 !!! | |
|
  | |
mt2sr
Maître

 Nombre de messages : 104 Nombre de messages : 104
Date d'inscription : 16/01/2006
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  Ven 01 Nov 2013, 16:43 Ven 01 Nov 2013, 16:43 | |
| la suite converge vers 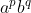 | |
|
  | |
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  Ven 01 Nov 2013, 20:22 Ven 01 Nov 2013, 20:22 | |
| BSR
pour quoi la suite converge et pour quoi sa limite est a^p.b^q
si la suite converge sa limite est supérieur ou égale à : a^p.b^q | |
|
  | |
Invité
Invité
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  Sam 02 Nov 2013, 09:00 Sam 02 Nov 2013, 09:00 | |
| Bonjour,
On commence par montrer que $a_n=1+(ln a)/n+o(1/n)$.
De même $b_n=1+(ln b)/n+o(1/n)$.
On en déduit que $p a_n+q b_n=1+(p ln a + q ln b)/n +o(1/n)$.
La limite de $n ln(p a_n+q b_n)$ est donc égale à $p ln a + q ln b$.
D'où enfin la limite de $(p a_n+q b_n)^n$ est égale à $a^p b^q$. |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  Sam 02 Nov 2013, 10:11 Sam 02 Nov 2013, 10:11 | |
| - aissa a écrit:
- lim (a_n)^n = a >0 et lim(b_n)^n = b > 0 !!!
Ah oui j'ai oublié les puissances hahaha! la solution de jandri est bonne Reste à vérifier le dvpt limité: a_n=1+(ln a)/n+o(1/n) pour lim (a_n)^n = a >0 on pose e_n=(a_n)^n-a --->0 a_n=(e_n+a)^(1/n) =exp( ln(e_n+a) /n) =exp(ln(a)/n + ln(1+e_n/a) /n) =exp(ln(a)/n + o(1/n)) =1+ln(a)/n +o(1/n) | |
|
  | |
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  Sam 02 Nov 2013, 10:15 Sam 02 Nov 2013, 10:15 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: suite réelle Sujet: Re: suite réelle  | |
| |
|
  | |
| | suite réelle |  |
|
