Etude d'une série:

Etudier la série de terme général .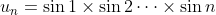
Bonne chance.

bonsoir nmo,
tres joli exo pour le resoudre j'utilise des fractions continu et grace a ca on a meme une convergence absolu ca intéresserai de savoir si il y a une methode plus simple

|u_(n+1)|=|u_n|.|sin(n+1)|=<|u_n|  ==> (|u_n|) décroissante ==> (|u_n|) converge vers u>=0
si u>0 ==> |sin(n+1)|--->1 ==> sin²(n)-->1 ==> cos²(n)=1-sin²(n)-->0
==> sin²(2n)=4sin²(n)cos²(n) -->0  absurde. Donc u_n--->0

-1=< u_(n+1)/u_n=sin(n+1)=<a<1 qqs n  ( on utilisera les réduites de pi)
si à partir d'un certain rang les u_n sont de même signe, la règle de D’Alembert assure la convergence
sinon il existe une sous suite (v_n) tel que v_n.v_(n+1)<0 , |v_(n+1)|=<|v_n| ==> série alternée convergente
soit (w_n) la sous suite de (u_n) en oubliant les (v_n) alors  |w_(n+1)/w_n|=<a
==> la série w_n est convergente (D’Alembert) ainsi la série u_n converge

si Un <1  qqs n ça veut dire pas qu'il existe a<1 tel que Un =<a qqs n !

ayoubmath a écrit:

si Un <1  qqs n ça veut dire pas qu'il existe a<1 tel que Un =<a qqs n  !

Désolé un tel a n'existe pas car 1 est une valeur d'adhérence de la suite (sin(n))

je donnerai une autre preuve

pour n>0, soit k_n=E[n/pi] <==> 0<n-k_n.pi<pi
on pose : v_n=sin(1-k_1.pi)...sin(n-k_n.pi)
(v_n) est une suite décroissante positive et de limite nulle car v_n=|u_n|
u_n=(-1)^K_n.v_n où K_n=k_1+...+k_n.
Par le critère d'Abel, pour que la série de terme général u_n converge il suffit de montrer que la suite
(somme(s=1 à n) (-1)^K_s )_n est bornée.

monsieur attioui pouvez vous expliquer pourquoi la somme est bornée ?

Bonjour ,

en utilisant l'inégalité arithmético-géométrique on a pour tout entier naturel non nul n ,

un^(²/n) = (sin²(1).sin²(2)...sin²(n))^(1/n) =< (sin²(1)+sin²(2)+...+sin²(n))/n

et il n'est pas dificile de montrer que la suite de droite converge vers 1/2 (en utilisant les complexes par exemple)

et ainsi si a est un réel strictement compris entre 1/2 et 1 , il existe un rang N à partir duquel on a , un^(²/n) =< a

ce qui donne , pour tout n>=N , |un| =< b^n où b est la racine carrée de a    sauf erreur bien entendu

oui
il y a plus simple entre sin(n),sin(n+1),sin(n+2),sin(n+3),sin(n+4),sin(n+5),sin(n+6) il y en a au moin un qui est plus petit en valeur absolue que 1/2 donc u_n=O(1/2^(n/7)) et c'est gagne.