younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: belle inegalite Sujet: belle inegalite  Lun 24 Fév 2014, 17:30 Lun 24 Fév 2014, 17:30 | |
| | |
|
Nas8
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 28
Date d'inscription : 26/11/2011
 |  Sujet: Re: belle inegalite Sujet: Re: belle inegalite  Lun 24 Fév 2014, 22:53 Lun 24 Fév 2014, 22:53 | |
| on prend b > a et c on posant x = a/b et y = c/b on trouve v(x²+y) + v(y²+x) + v(1+xy) < 3/2 ( x+y+1) il suffit de la demontré avec 0 < x et y < 1 je pense qu'avec 2 inconnu cela sera plus facile  je manque de temps , j'essayerai de continuer plus tard . | |
|
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: belle inegalite Sujet: Re: belle inegalite  Lun 24 Fév 2014, 23:29 Lun 24 Fév 2014, 23:29 | |
| - Nas8 a écrit:
- on prend b > a et c
on posant x = a/b et y = c/b on trouve
v(x²+y) + v(y²+x) + v(1+xy) < 3/2 ( x+y+1) il suffit de la demontré avec 0 < x et y < 1
je pense qu'avec 2 inconnu cela sera plus facile  je manque de temps , j'essayerai de continuer plus tard . je manque de temps , j'essayerai de continuer plus tard .
je pense que votre ineq est vrai pr tt x,y>0 si a >b >c prend a=bx,c=by on trouve la mm inégalité avec la condition x >1 >y>0 et aussi la mm inégalité avec la condition x,y > 1 si en prend b <min{a,c}. | |
|
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: belle inegalite Sujet: Re: belle inegalite  Dim 02 Mar 2014, 18:40 Dim 02 Mar 2014, 18:40 | |
| personne n'a donne une reponse....!!!!!! | |
|
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: belle inegalite Sujet: Re: belle inegalite  Dim 02 Mar 2014, 22:17 Dim 02 Mar 2014, 22:17 | |
| posons a >b >c on a : 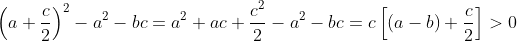 alors : 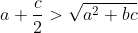 maintenant il reste de démontrer que 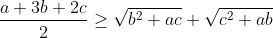 on a : 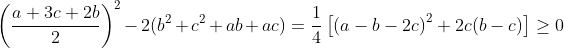 donc : 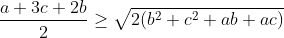 Selon Caushy : 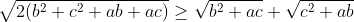 alors : 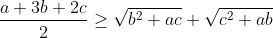 Conclusion : 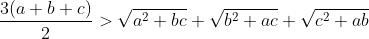 l’égalité se trouve quand c=0 et a=b et puisque a,b,c>0 alors il n’y a pas d'égalité. P.S : j'ai trouvé cette solution dans un livre  | |
|
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: belle inegalite Sujet: Re: belle inegalite  Mar 05 Aoû 2014, 19:07 Mar 05 Aoû 2014, 19:07 | |
| | |
|
Contenu sponsorisé
 |  Sujet: Re: belle inegalite Sujet: Re: belle inegalite  | |
| |
|
