limite "Chaude"

Calculer lim (x-->a) (sin²x-cosx*sinx)/(x²-a²)

j'ai distinguéles cas !!! mais trés vaste   

une autre
lim x----0 f(x) tel que :
f(x)=(x-sin(x))/(x-tan(x))

(Sans DL )

personne ? ....

Salam,
Pour la première comme tu l'as dit il faut discuter les cas suivant la valeur de a, la limite a ce que je vois,peut avoir pour valeur: 0, "une valeur en fonction de pi", ou FI (un truc sur zéro).
Pour la deuxième tu peux diviser le numérateur et le dénominateur par x^3 et tu cherches les deux limites (ça existe déjà sur le forum).

pr le 2éme ça donne rien j'ai encore une forme indéterminé   

tu dois calculer chaque limite a part et comme je t'ai dit les deux sont traite ça fait je pense une année ou deux ans sur ce forum.

j'ai pas compris :p comment tu peux calculer chaque limite à part !

j'ai essayé mais tout sans vain   

j'ai la solution par DL mais je cherche une démarche simple et bien truqué   

tu cherches lim x----0 f(x) tel que :
f(x)=(x-sin(x))/x^3

et lim x----0 f(x) tel que :
f(x)=x^3/(x-tan(x))

pour la dernière tu peut utiliser la première et je te dit encore que juste tu cherches dans le forum si tu trouves pas on peut les trouver encore, et cela dit sans DL.
Deja tu connais DL c'est bien.

M. P_Coelho a écrit :
Calculer lim (x-->a) (sin²x-cosx*sinx)/(x²-a²)
j'ai distinguéles cas !!! mais trés vaste

Cette limite ne est du domaine de M. Legend_Crush, qui est un expert en la matière, et qui par ses remarques pertinentes m'a aidé plusieurs fois à résoudre des problèmes très difficiles.

En ce qui concerne l'étude de cette limite, je propose la démarche suivante qui ne sera valable sans l'aval de M. Legend_Crush ou l'un de nos maîtres du "Site" : 

 

aymane, est ce que t'as essayé de calculer la limite en pi par exemple?

waw c génial ! merci bcpp Aymeen

Je doute qu'il y ai un erreur d'inattention dans la sixième ligne, enfin je crois ^^, vu que tu a x²-a² au dénominateur et pas x-a.

Sauf Erreur
Concernant la deuxième limite, je crois aussi qu'on doit diviser et multiplier par x^3. J'ai pu en effet calculer lim(x->0) (sinx-x)/x^3=-1/6 grace à un encadrement mais je n'ai pas pu trouver lim(x->0) x^3/x-tan(x)

M. Legend_Crush, j'ai rectifié mon message initial: j'espère qu'il n y a pas d'autres erreurs.

Une seule petite remarque, la dérivée est PEUT-ETRE fausse
ça doit être, selon Wolframalpha, sin(2x)-cos(2x) ce qui est différent de la formule que vous avez trouvé :p

tu parles du numérateur bien sur

legend-crush a écrit:

Je doute qu'il y ai un erreur d'inattention dans la sixième ligne, enfin je crois ^^, vu que tu a x²-a² au dénominateur et pas x-a.

Sauf Erreur
Concernant la deuxième limite, je crois aussi qu'on doit diviser et multiplier par x^3. J'ai pu en effet calculer lim(x->0) (sinx-x)/x^3=-1/6 grace à un encadrement :Dmais je n'ai pas pu trouver lim(x->0) x^3/x-tan(x)

Il faut mentionner en premier temps que ...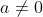
Pour ce qui est de la dernière limite, on peut procéder ainsi: .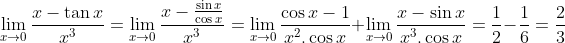
Sauf erreurs.

Pour ce sujet, on a vraiment de la chance: la présence d'un maître et d'un expert nous rassure et nous évite de nous égarer sans guides ni conseillers: je vous remercie Messieurs Légend_Crush et Nmo.

En ce qui concerne l'exercice, je porte à votre connaissance que j'ai pris en considération la remarque de M. Legend_Crush en ce qui concerne la dérivée du numérateur, quant à la remarque de M. Nmo, j'attire votre attention que j'ai entamé ma démonstration en étudiant le cas où "a=0", puis j'ai travaillé sur Z* pour les "k pairs".

J'espère que vous trouveriez un peu de temps, pour colmater les brèches de ma démarche, ce qui permettra d'offrir aux visiteurs de cette page une solution de cet exercice au niveau du groupe qui s y anime.

Pour finir, je lance un appel à nos Maîtres "Ahmed_TAHA" , "L_W_P" , "BIANCO_VERDE" et tous les autres qui depuis plusieurs jours ne se sont pas activés sur le Site: je leur dis que leurs remarques et leurs conseils nous manquent beaucoup.