| | Derivation |  |
|
|
| Auteur | Message |
|---|
Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Derivation Sujet: Derivation  Lun 17 Mar 2014, 08:33 Lun 17 Mar 2014, 08:33 | |
| déterminer la fonction polynome f du 3éme degree tel que : 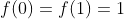 et 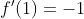 et 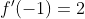 | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Derivation Sujet: Re: Derivation  Lun 17 Mar 2014, 09:48 Lun 17 Mar 2014, 09:48 | |
| Soit f(x) = a x^3 + b x^2 + c x + d, avec (a;b;c;d) appartenant à IR4;
donc f'(x) = 3 a x^2 + 2 b x + c.
On a: f(0) = 1 --> d=1.
On a aussi f(1) = a + b + c + d = a + b + c + 1 = 1
--> f(1) = a + b + c = 0
f'(1) = 3 a + 2 b + c = -1
f'(-1) = 3 a - 2 b + c = 2
C'est un système d'équations qui donne que : a = - 1/8 ; b = - 3/4 et c = 7/8,
donc f(x) = -1/8 x^3 -3/4 x^2 +7/8 x + 1 . | |
|
  | |
Amiral
Maître

 Nombre de messages : 94 Nombre de messages : 94
Age : 27
Localisation : la maison
Date d'inscription : 11/03/2014
 |  Sujet: Re: Derivation Sujet: Re: Derivation  Lun 17 Mar 2014, 12:56 Lun 17 Mar 2014, 12:56 | |
| bravo ^^ j'espere qu'il y a une autre solution ,on laisse la chance pr les autres  | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Derivation Sujet: Re: Derivation  Lun 17 Mar 2014, 17:36 Lun 17 Mar 2014, 17:36 | |
| je suis arrivé avec la même démo de MR aymanemaysae, et je pense que c'est la méthode la plus classique et peut être la plus utilisée pour atteindre à la solution.
comme petite remarque il faut mentionner que a=/=0 pour qu'on aura une fonction de 3 degré | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Derivation Sujet: Re: Derivation  Lun 17 Mar 2014, 23:07 Lun 17 Mar 2014, 23:07 | |
| Merci M. L-W-P, pour la remarque: pour moi elle est essentielle, car la plupart du temps, j'oublie de mentionner ces précisions, et cela me cause beaucoup de tort et beaucoup de désagrément.
Merci encore une fois.
Dernière édition par aymanemaysae le Mar 18 Mar 2014, 12:59, édité 1 fois | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Derivation Sujet: Re: Derivation  Mar 18 Mar 2014, 12:18 Mar 18 Mar 2014, 12:18 | |
| f(x) = a x(x-1)² + b x(x-1)+ c x + d car {1,x,x(x-1),x(x-1)²} base puisque de degrés échelonnes
f(0)=d=1
f(1)= c+d=1 ==> c=0
f'(x)=a(3x²-4x+1)+b(2x-1)
f'(1)=b=-1
f'(-1)=8a-3b=2 ==> a= -1/8
donc f(x)=-x(x-1)²/8 - x(x-1)+1
Dernière édition par abdelbaki.attioui le Mer 19 Mar 2014, 08:29, édité 1 fois | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Derivation Sujet: Re: Derivation  Mar 18 Mar 2014, 13:35 Mar 18 Mar 2014, 13:35 | |
| Bonjour M. Abdelbaki_Attioui, avant tout veuillez excuser la présence de ses deux "Smileys": je ne sais pas d'où ils sortent: ils masquent un "huit". f(x) = (1/8)x(x-1)^2 - x(x+1) + 1 , donc f'(x) = (1/  ((x-1)^2 + 2x(x-1)) - (x+1) - x , donc f'(-1)= (1/  ( 4 + 4 ) + 2 +1 = 4 et non 2 comme dans l'énoncé de l'exercice. Veuillez m'excuser si j'ai commis une faute et si ma remarque est déplacée. De toute façon, la méthode utilisée ouvre le chemin vers d'autres horizons et d'autres possibilités pour aborder des problèmes du même genre mais plus difficile à résoudre. Merci beaucoup. | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Derivation Sujet: Re: Derivation  Mer 19 Mar 2014, 08:30 Mer 19 Mar 2014, 08:30 | |
| - aymanemaysae a écrit:
- Bonjour M. Abdelbaki_Attioui, avant tout veuillez excuser la présence de ses deux "Smileys": je ne sais pas d'où ils sortent: ils masquent un "huit".
f(x) = (1/8)x(x-1)^2 - x(x+1) + 1 ,
donc f'(x) = (1/ 8 )((x-1)^2 + 2x(x-1)) - (x+1) - x ,
donc f'(-1)= (1/ 8 )( 4 + 4 ) + 2 +1 = 4 et non 2 comme dans l'énoncé de l'exercice.
Veuillez m'excuser si j'ai commis une faute et si ma remarque est déplacée.
De toute façon, la méthode utilisée ouvre le chemin vers d'autres horizons et d'autres possibilités pour aborder des problèmes du même genre mais plus difficile à résoudre.
Merci beaucoup. Bien vu a=-1/8 pour les Smileys ajouter un espace entre 8 et ) | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: Derivation Sujet: Re: Derivation  Mer 19 Mar 2014, 09:35 Mer 19 Mar 2014, 09:35 | |
| Merci M. Abdelbaki-Attioui pour l'astuce qui permet d'empêcher les smileys d'apparaitre.
Bonne journée. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Derivation Sujet: Re: Derivation  | |
| |
|
  | |
| | Derivation |  |
|
