inégalité avec la fonction exp

Montrer que, pour tous réels a, b, c tels que a < b < c et tout réel x,

exp(bx) ≤ exp(ax) + exp(cx)

abdelbaki.attioui a écrit:: Montrer que, pour tous réels a, b, c tels que a < b < c et tout réel x,

exp(bx) ≤ exp(ax) + exp(cx)

Puisque 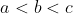$inégalité avec la fonction exp Gif$ , il existe 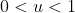$inégalité avec la fonction exp Gif$ tel que $inégalité avec la fonction exp Gif$ .
La convexité de la fonction exponentielle et la définition de 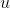$inégalité avec la fonction exp Gif$ permettent d'écrire que: $inégalité avec la fonction exp Gif$ .
Sauf erreurs!

très jolie preuve mmo

Voici une autre approche
C'est équivalent à montrer exp((b-a)x)=<exp((c-a)x)+1, pour tout x dans R et c-a>b-a>0.
Si x>=0, exp((b-a)x)=<exp((c-a)x)=<exp((c-a)x)+1.
Si x<0, exp((b-a)x)=<1=<exp((c-a)x)+1,

» Inégalité avec a_i, a_j € R*.
» inégalité avec cos et sin
» inegalité avec logarithme Ln
» inégalité avec des intégrals
» inégalité avec sinus