Aide pour un DM de maths

Je voulais simplement me donner des petites indications, si vous pouviez m'éclairer un peu

Je
vais vous donner les questions de mon DM et ce que j'ai répondu, si une
de mes réponses vous semble un peu tordue, dites le moi

(Ma réponse = mrp)

Soit ABC un triangle rectangle en C avec AB = 10 cm et BC = 6 cm. Soit E un point de [BC] tel que BE = x. EFGC est un rectangle.

Triangle :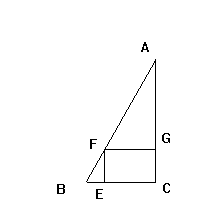



1. Calculer AC

mrp :

Code:

ABC
est un triangle rectangle en C or dans un triangle rectangle , le carré
de l'hypothénuse est égal à la somme des carrés des deux autres côtés
donc : AB^2 = AC^2 + BC^2
AC^2 = AB^2 - BC^2
AC^2 = 100 - 36
AC = racine(64)
AC = 8

2. (a) : Quelles sont les valeurs possibles de x ?

mrp :

Code:

BC = 6 cm et E appartient à [BC] donc x = BC - EC

(b) Exprimer EC en fonction de x

mrp :

Code:

Comme E appartient à [BC], les points B,E et C sont alignés et BE = x donc EC = BC - x

(c) Exprimer EF en fonction de x.

mrp :

Code:

FGCE est un rectangle, que les 4 côtés d'un réctagnle sont des angles droits et que E appartient au triangle FBE, l'angle E est un angle droit de plus comme E appartient à FBE, le triangle FBE est rectangle en E, or dans un triangle rectangle, le carré de l'hypothénuse est égale à la somme des carrés des 2 autre côtés donc FB^2 = BE^2 + FE^2
FE^2 + FB^2 - BE^2
FE = racine(FB) - racine(BE)

(d) Pour quelle valeur de x le rectangle est-il un carré :

Code:

Aucune idée, si vous pouviez m'aider ?

3.(a) Calculer en fonction de x le périmètre P(x) du réctangle EFGC

Code:

Idem, je ne comprend pas où je peux avoir la formule P(x)

(b) Pour quelle valeur de x a-t-on P(x) = 13 ?

Code:

sans la formule P(x), je ne peux pas faire grand chose

4.(a) Montrer que l'air du rectangle EFGC est donnée par :
a
A(x) = 4/3*x*(6 - x)

Code:

?, aucune idée

(b) Calculer A(0) et A(6). Vérifier géométriquement ce résultat.
(c) Complétez le tableau de valeurs suivant :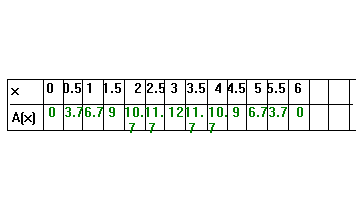

Code:

Les textes en noir sont du DM et les verts c'est moi !

(f) Déterminer le max de la fonction A et donner la valeur x correspondante à partir du graphique

Code:

je voulais juste savoir le max de la fonction A c'est y donc en ordonnée ? et x en absisse c'est cela ?

Exercice 2 :

Résoudre les équations suivantes :

1) (3x - 2)^2 = 9(x - 4)^2

Code:

(3x - 2)^2 - 9(x - 4)^2 = 0
[(3x - 2) + 9(x - 4)] [(3x - 2) - 9(x - 4)]
(10x - 36) (-8x + 36) = 0
Si AB = 0 alors A = 0 ou B = 0 donc :
x = 36/10 ou x = 36/8
S = {36/10 ; 36/8}

2) (3x - 4) (x + 1) = 3x^2 + 4

Code:

(3x - 4) (x + 1) - 3x^2 - 4 = 0
(3x - 4) (x + 1) - (3x - 4) (3x + 4)
(3x - 4) [x + 1 - 3x - 4]
(3x - 4) (-2x - 3)
Si AB = 0 alors A = 0 ou B = 0 donc :
x = 4/3 ou x = - 3/2
S = {4/3; - 3/2}

3) (4x^2 - (x + 1)^2)/(4x(x+1)) = 0

Code:

Valeurs interdites pour x :
4x(x+1) = 0
Si AB = 0 alors A = 0 ou B = 0 donc :
x = 0 ou x = -1
Les valeurs interdites pour x sont : {0; -1}
Si A/B = 0 alors A = 0 donc :
4x^2 - (x+1)^2 = 0
[4x - (x+1)] [4x + (x+1)] = 0
(3x + 1) (5x + 1) = 0
Si AB = 0 alors A = 0 ou B = 0 donc :
x = - 1/3 ou x = -1/5
Comme - 1/3 et -1/5 est différent de -1 et de 0 donc :
S = {-1/3 ; -1/5)

4) 2x + 7 = 4/(2x +7)

Code:

J'ai pas réussi celui là, si quelqu'un peut m'aider ?

salut

c) Exprimer EF en fonction de x.
c'est dans cette question ou tu dois résoudre le problème si tu trouves EF en fonction de x le problème est résolu

et pour P(x)=2(x+la réponse de 2.c)
essaye de revoir ton exo

C 'est pas bon ce que j'ai mis :

Code:

(c) Exprimer EF en fonction de x.

mrp :
Code:
FGCE est un rectangle, que les 4 côtés d'un réctagnle sont des angles droits et que E appartient au triangle FBE, l'angle E est un angle droit de plus comme E appartient à FBE, le triangle FBE est rectangle en E, or dans un triangle rectangle, le carré de l'hypothénuse est égale à la somme des carrés des 2 autre côtés donc FB^2 = BE^2 + FE^2
FE^2 + FB^2 - BE^2
FE = racine(FB) - racine(BE)

Sinon pour le reste vous pouvez m'aider un peu ?

Quelqu'un a une idée

Mais où sont les matheux ?

non
pour(c)
on a x/BC=EF/AC (TALLES)
EF=ACx/bc=8x/6
EF=4x/3

pour que se soit un caree il faut que EF=EC
4x/3=6-x
7x/3=6
donc x=18/7

p(x)=(EF+EC)*2=(4x/3+6-x)*2
p(x)=2x/3+12

p(x)=13
2x/3+12=13
2x/3=1
x=3/2

A(x)= l'air=EF*EC=4x/3*(6-x)
o taba9i kmel mnrassek

Merci pour tout, sinon j'ai un petit blem (voir partie "exercice 2" sur les equations, merci !

(3x - 2)^2 - 9(x - 4)^2 = 0
[(3x - 2) + 9(x - 4)] [(3x - 2) - 9(x - 4)]=0 faux
[(3x - 2) + 3(x - 4)] [(3x - 2) - 3(x - 4)]=0

la 2eme la meme erreur du 1
la 3eme khass tableau des signes

la 4eme
2x+7=4/2x+7 (2x+7≠0 alors x≠-7/2)
(2x+7)²=4
2x+7=-2 ou 2x+7=2
x=-9/2 ou x=-5/2

Merci pour tout, vraiment excellent, je vais voir mes erreurs , merci encore

de rien c'est avec plaisir