yassine-mansouri
Expert grade1

 Nombre de messages : 426 Nombre de messages : 426
Age : 34
Localisation : Tetouan
Date d'inscription : 18/02/2007
 |  Sujet: demontrer que ............... Sujet: demontrer que ...............  Ven 22 Juin 2007, 19:12 Ven 22 Juin 2007, 19:12 | |
| on designe par a,b et c les longueurs des cotés d'un triangle .
Demontrer que
a²(b+c-a)+b²(a+c-b)+c²(a+b-c)=<3abc | |
|
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: demontrer que ............... Sujet: Re: demontrer que ...............  Dim 24 Juin 2007, 11:38 Dim 24 Juin 2007, 11:38 | |
| salut tout le monde. 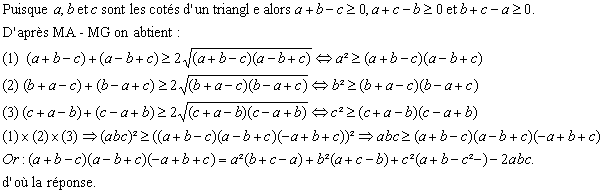 | |
|
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: demontrer que ............... Sujet: Re: demontrer que ...............  Mar 26 Juin 2007, 12:25 Mar 26 Juin 2007, 12:25 | |
| comme a ,bet c sont les coté dun triangle , alors on peut poser , a+b-c=2x , b+c-a=2y et c+a-b=2z .... ce qui réduit considérablement le ravail! | |
|
yassine-mansouri
Expert grade1

 Nombre de messages : 426 Nombre de messages : 426
Age : 34
Localisation : Tetouan
Date d'inscription : 18/02/2007
 |  Sujet: Re: demontrer que ............... Sujet: Re: demontrer que ...............  Mar 26 Juin 2007, 13:21 Mar 26 Juin 2007, 13:21 | |
| - boukharfane radouane a écrit:
- salut tout le monde.
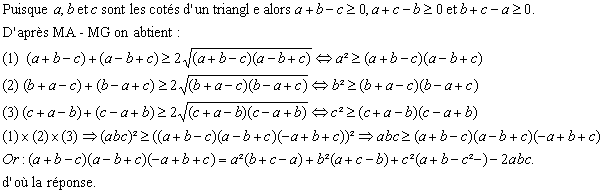 c tres bien fait !! | |
|
yassine-mansouri
Expert grade1

 Nombre de messages : 426 Nombre de messages : 426
Age : 34
Localisation : Tetouan
Date d'inscription : 18/02/2007
 |  Sujet: Re: demontrer que ............... Sujet: Re: demontrer que ...............  Mar 26 Juin 2007, 13:22 Mar 26 Juin 2007, 13:22 | |
| - o0aminbe0o a écrit:
- comme a ,bet c sont les coté dun triangle , alors on peut poser , a+b-c=2x , b+c-a=2y et c+a-b=2z .... ce qui réduit considérablement le ravail!
c ma methode ! | |
|
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: demontrer que ............... Sujet: Re: demontrer que ...............  Sam 14 Juil 2007, 22:23 Sam 14 Juil 2007, 22:23 | |
| - yassine-mansouri a écrit:
- o0aminbe0o a écrit:
- comme a ,bet c sont les coté dun triangle , alors on peut poser , a+b-c=2x , b+c-a=2y et c+a-b=2z .... ce qui réduit considérablement le ravail!
c ma methode ! non cest celle de ravi  | |
|
yassine-mansouri
Expert grade1

 Nombre de messages : 426 Nombre de messages : 426
Age : 34
Localisation : Tetouan
Date d'inscription : 18/02/2007
 |  Sujet: Re: demontrer que ............... Sujet: Re: demontrer que ...............  Lun 16 Juil 2007, 13:40 Lun 16 Juil 2007, 13:40 | |
| | |
|
Contenu sponsorisé
 |  Sujet: Re: demontrer que ............... Sujet: Re: demontrer que ...............  | |
| |
|
