| | test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) |  |
|
+13mathema ouwais graziella JASPER rajaa16 radouane_BNE mahmoud16 Fourrier-D.Blaine Alaoui.Omar iverson_h3 kalm Conan samir 17 participants |
|
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 | |
  | |
Invité
Invité
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mar 12 Fév 2008, 20:27 Mar 12 Fév 2008, 20:27 | |
| exo1 cet exo est presque trivial , si ABC est un triangle rectangle ( supposons qu'en A) alors sin²A=1 ( car A= pi/2), et puisque B+C= pi/2 ==> sin²B+sin²C= cos²C+sin²C= 1 , d'ou le résultat exo2: je propose comme valeur max : 1/4 ona : max(-2xyz)= 0 , et 0 est atteint si seulement si x ou y ou z=0 supposons alors que c'est x ona : max( xy+yz+xz)= max( yz)= max( (y+z)²/4) = 1/4 d'ou le résultat, exo3: ( un très joli exo qui m'a plus  , mais je vois que le fait que (x,y,z,t) £ ( 1/2, +OO) est une condition pas nécessaire) ona : abcd < (a+b+c+d)^4/256 ( IAG), et abcd> a²+b²+c²+d²>(a+b+c+d)²/4 ( cauchy-shwarz), alors : (a+b+c+d)^4/256 > (a+b+c+d)²/4 <=> (a+b+c+d)²>68, ==> a+b+c+d>8donc abcd> (a+b+c+d)²/4 = (a+b+c+d)/4 * (a+b+c+d) > 2(a+b+c+d)=a+b+c+d+a+b+c+d > a+b+c+d+8 C.Q.F.D (sauf ereur de ma part) A+ |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mar 12 Fév 2008, 23:45 Mar 12 Fév 2008, 23:45 | |
| pour l'exo 1 tu dois faire neutrino l'autre implication
pour le 2éme exo , on a : p=<1
et sachant que selon Shurr q =< (p^3+9r)/4p
donc : q-2r =< (p^3 - 8pr + 9r)/4p = f(p)
et on a : f'(p) = (8p^3-36r)/4p² >= 0 car p^3 >= 27r
alors
q-2r=< f(p) =< f(1) = (r+1)/4 =<((p^3/27)+1)/4 =< (1/27+1)/4 = 7/27
Dernière édition par le Mer 13 Fév 2008, 08:37, édité 1 fois | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 13 Fév 2008, 00:12 Mer 13 Fév 2008, 00:12 | |
| on a : ABC rectangle => sin²a + sin²b + sin²c = 2 trivial
mnt supposon que sin²a + sin²b + sin²c = 2
alors 1-2sin²a + 1-2sin²b + 1-2sin²c = -1
donc cos 2b + cos 2c + cos 2a = -1 (A)
or cos2b + cos2c + cos2a = 2cos(b+c)*cos(b-c) + cos2a
= -2cos(a)*cos(b-c) + 2cos²(a) - 1
= -2cos(a)(cos(b-c)+cos(b+c)) - 1
= -4 cos(a) cos(b) cos(c) - 1 (B)
de A et B on déduit que cos(a) cos(b) cos(c) = 0 d'ou le résultat
Dernière édition par le Mer 13 Fév 2008, 08:42, édité 1 fois | |
|
  | |
kalm
Expert sup

Nombre de messages : 1101
Localisation : khiam 2
Date d'inscription : 26/05/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 13 Fév 2008, 00:22 Mer 13 Fév 2008, 00:22 | |
| - Conan a écrit:
- pour l'exo 1 tu dois faire neutrino l'autre implication
pour le 2éme exo , on a : p=<1
et sachant que selon Shurr q =< (p^3+9r)/4p
donc : q-2r =< (p^3 - 8pr + 9r)/4p = f(p)
et on a : f'(p) = (8p^3-36r)/4p² >= 0 car p^3 >= 27r
alors
q-2r=< f(p) =< f(1) = (5r+1)/4 =<(5(p^3/27)+1)/4 =< (5/27+1)/4 = 8/27 c faux | |
|
  | |
kalm
Expert sup

Nombre de messages : 1101
Localisation : khiam 2
Date d'inscription : 26/05/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 13 Fév 2008, 00:23 Mer 13 Fév 2008, 00:23 | |
| - neutrino a écrit:
- exo1
cet exo est presque trivial , si ABC est un triangle rectangle ( supposons qu'en A) alors sin²A=1 ( car A= pi/2), et puisque B+C= pi/2 ==> sin²B+sin²C= cos²C+sin²C= 1 , d'ou le résultat
exo2:
je propose comme valeur max : 1/4
ona : max(-2xyz)= 0 , et 0 est atteint si seulement si x ou y ou z=0
supposons alors que c'est x
ona : max( xy+yz+xz)= max( yz)= max( (y+z)²/4) = 1/4 d'ou le résultat,
exo3: ( un très joli exo qui m'a plus  , mais je vois que le fait que (x,y,z,t) £ ( 1/2, +OO) est une condition pas nécessaire) , mais je vois que le fait que (x,y,z,t) £ ( 1/2, +OO) est une condition pas nécessaire)
ona : abcd < (a+b+c+d)^4/256 ( IAG), et abcd> a²+b²+c²+d²>(a+b+c+d)²/4 ( cauchy-shwarz),
alors : (a+b+c+d)^4/256 > (a+b+c+d)²/4
<=> (a+b+c+d)²>68, ==> a+b+c+d>8
donc abcd> (a+b+c+d)²/4 = (a+b+c+d)/4 * (a+b+c+d) > 2(a+b+c+d)=a+b+c+d+a+b+c+d > a+b+c+d+8 C.Q.F.D
(sauf ereur de ma part)
A+ c faux pour le 2 exo | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 13 Fév 2008, 08:39 Mer 13 Fév 2008, 08:39 | |
| regarde mieux Kalm c'etais simplement une faute de frappe  | |
|
  | |
iverson_h3
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 08/09/2007
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 13 Fév 2008, 12:02 Mer 13 Fév 2008, 12:02 | |
| slt !!!!!!!!
pr l'ex 3 voici ce que g trouvé :
on pose a>=b>=c>=d, en applicant chebybev on trouve :
a²+b²+c²+d²>=(a+b+c+d)²/4>= 4V(abcd) "IAG"
et on a : 2V(abcd) >= 2V(a²+b²+c²+d²) >=a+b+c+d
et : 2V(abcd)>= 8
car : a²+b²+c²+d²>=4Vabcd "IAG"
<=> abcd>=4V(abcd) <=> V(abcd)>=4
donc : abcd>= a²+b²+c² >= 4V(abcd)>= a+b+c+d+8
@+
NB : je pense qu'il y a qlq chose qui cloche ds ma solution, sinon pk a,b,c,d £ (1/2,+oo) | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 13 Fév 2008, 13:33 Mer 13 Fév 2008, 13:33 | |
| | |
|
  | |
Fourrier-D.Blaine
Expert grade2

 Nombre de messages : 302 Nombre de messages : 302
Date d'inscription : 21/12/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 13 Fév 2008, 22:16 Mer 13 Fév 2008, 22:16 | |
| EXERCICE 1 is very trivial since we have in any triangle:  | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 | |
  | |
Fourrier-D.Blaine
Expert grade2

 Nombre de messages : 302 Nombre de messages : 302
Date d'inscription : 21/12/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Jeu 14 Fév 2008, 19:11 Jeu 14 Fév 2008, 19:11 | |
| | |
|
  | |
mahmoud16
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 34
Date d'inscription : 31/12/2005
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Jeu 14 Fév 2008, 20:52 Jeu 14 Fév 2008, 20:52 | |
| pour l'exo 2 , remarquons que min(x,y,z) <=1/2 notons x se min par exemple et posons t(x,y,z) =xy+yz+zx-2xyz alors par un calcul simple
t(x,y,z)=<t(x,(y+z)/2,(y+z)/2) =<t(x,(1-x)/2,(1-x)/2)=g(x)
par etude de cette derniere fonction sa grande valeur ds [0,1/2] vaut 7/27
et les inegalités devient des egalités donc t=7/27 et c pour x=y=z=1/3 | |
|
  | |
mahmoud16
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 34
Date d'inscription : 31/12/2005
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Jeu 14 Fév 2008, 21:00 Jeu 14 Fév 2008, 21:00 | |
| pour le troisieme par l'absurde si abcd <= a+b+c+d alors par l'hypothese et cauchy shwartz on trouve que a+b+c+d<=4 ( une inequation de second degré dont l'inconnu est a+b+c+d) et donc abcd<=1
mais d'autre part abcd >a^2+b^2+....>=1/4+1/4+1/4+1/4=1 ce qui donne une contradiction . | |
|
  | |
Fourrier-D.Blaine
Expert grade2

 Nombre de messages : 302 Nombre de messages : 302
Date d'inscription : 21/12/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Ven 15 Fév 2008, 09:25 Ven 15 Fév 2008, 09:25 | |
| EXERCICE 2:     Et P(z) a 7/27 comme max (a voir avec la dérivation) et pour x=y=z=1/3 on a T=7/27 Proof complete. apparemen tt le monde haie la geométrie  | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Sam 08 Mar 2008, 21:02 Sam 08 Mar 2008, 21:02 | |
| salut tout le monde,apparemment les Marocaines n'excelllent que dans les inégalités et ne s'interessent plus à la géométrie mèmes d'apres ce que j'ai pu constater,les exos de la géométrie dans tous les OM precedents sont à la porté et abordables par contre les inégalités parfois sont difficles et presques parfois inabordables mèmes.Alors juste une petite conseil(mèe si je suis pas à la hauteur de ce conseil) pour les futurs participants et les representans du Maroc,j'espere qu'il essaye de mieux travailler et bosser dans la géométrie car surment ilss vont gagner bcp de points. | |
|
  | |
rajaa16
Maître

 Nombre de messages : 262 Nombre de messages : 262
Age : 32
Date d'inscription : 27/03/2008
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Ven 28 Mar 2008, 11:33 Ven 28 Mar 2008, 11:33 | |
| c'est des olympiades pour quek niveau?? | |
|
  | |
JASPER
Maître

 Nombre de messages : 100 Nombre de messages : 100
Age : 34
Localisation : La banquise
Date d'inscription : 13/06/2007
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Ven 28 Mar 2008, 12:03 Ven 28 Mar 2008, 12:03 | |
| | |
|
  | |
graziella
Débutant
 Nombre de messages : 3 Nombre de messages : 3
Age : 33
Date d'inscription : 04/04/2008
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Sam 05 Avr 2008, 15:34 Sam 05 Avr 2008, 15:34 | |
| j'ai r1 pigé lol c trop difficile et je suis encore nouvele au domaine!! [img][/img]   | |
|
  | |
graziella
Débutant
 Nombre de messages : 3 Nombre de messages : 3
Age : 33
Date d'inscription : 04/04/2008
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Sam 05 Avr 2008, 15:36 Sam 05 Avr 2008, 15:36 | |
| et en fait j ' y est participé et j'ai résolu qlq trucs!!!hhhhh | |
|
  | |
ouwais
Débutant
 Nombre de messages : 4 Nombre de messages : 4
Age : 31
Date d'inscription : 29/04/2008
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 30 Avr 2008, 15:54 Mer 30 Avr 2008, 15:54 | |
| mai j compren po commen vs avez fait pr lexo 3 vs ecrivez abcd> a²+b²+c²+d²>(a+b+c+d)²/4 plz repondez ^^ merci | |
|
  | |
mathema
Expert sup

 Nombre de messages : 922 Nombre de messages : 922
Age : 37
Localisation : Würzburg (Allemagne)
Date d'inscription : 19/07/2008
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Dim 20 Juil 2008, 02:48 Dim 20 Juil 2008, 02:48 | |
| Ce Olympiade de quel niveau????????????? | |
|
  | |
Ayem
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 35
Localisation : Caza
Date d'inscription : 02/05/2008
 | |
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 24 Aoû 2011, 17:16 Mer 24 Aoû 2011, 17:16 | |
| Désolé de revivre ce sujet mais j'ai essayé avec cette épreuve du stage et voici mes solutions aux problèmes  . Solution au problème 1:- Spoiler:
Montrons la première implication : ABC est un triangle rectangle => sin²A+sin²B+sin²C=2, ceci est immédiat vu que l'un des sinus vaut 1 et pour les deux autres angles le cosinus de l'un vaut le sinus de l'autre et en tenant compte du fait que pour tout x £ IR nous avons cos²x+cos²y =1 alors on conclut.
Pour la deuxième implication qui est plus intéressante :
Si sin²A+sin²B+si²C=2 alors cela est équivaleà cos²B+cos²C=sin²A=sin²(B+C) ce qui donne cosBcosC(cosBcosC-sinBsinC)=0, si l'un des cosinus est nul alors on tire immédiatement la conclusion,sinon alos oen élevant au carré on retrouve :sin²+sin²C=1=2-sin²A et ainsi sinA=1 alors dans ce cas aussi ABC est rectangle.
Finalement ABC est un triangle rectangle si et seulement si sin²A+sin²B+sin²C=2.
Solution au problème 2:- Spoiler:
Sans nuire à la généralité du problème on suppose que x=min{x,y,z} ainsi x<=1/3. Nous avons : +yz(1-2x)\leq&space;x(1-x)+\frac{(1-x)^2}{4}(1-2x)=\frac{-2x^3+x^2+1}{4}) . On se propsoe de montrer que la valeur maximale est 7/27 alors il suffit de prouver que : ^2(x+\frac{1}{6})\geq&space;0) . Ce qui est clairement vrai. Et puisque la valeur 7/27 est atteinte lorsque x=y=z=1/3 alors c'est la valeur recherchée .
Solution au problème 3:- Spoiler:
Par C.S + I.AG on obitent directement cette série d'inégalités : ^4>&space;abcd>&space;\sum&space;a^2>&space;\frac{1}{4}(\sum&space;a)^2>&space;4\sqrt{abcd}) . Ainsi on obtient a+b+c+d >=8 et ^2) . Donc il suffit de prouver que : 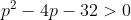 où 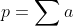 . Ce qui est clairement vrai puisque c'est équivalent : (p-8 )(p+4)>0
Solution au problème 4:- Spoiler:
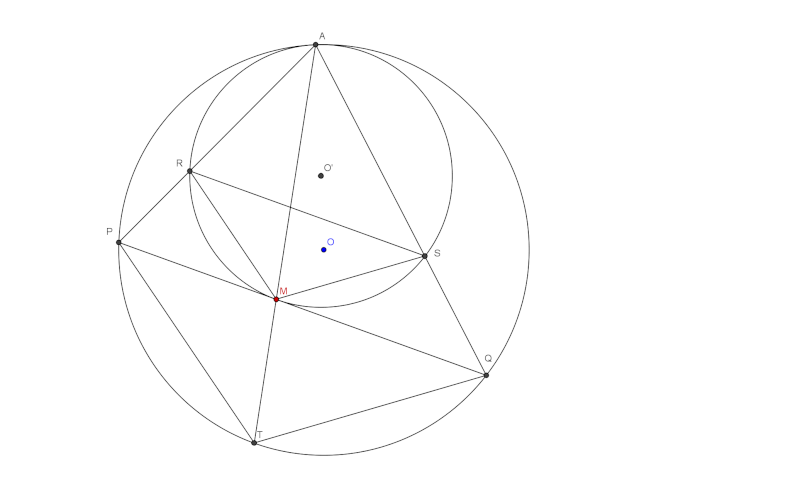 Notons R et S les points d'intersections de AP et AQ avec (C'), T celui de AM avec(C). Il est bien clair que angle{MAQ}=angle{TAS}=angle{MAS}=angle{QMS}=angle{QMA}-angle{AMS}=angle{QMA}-angle{APQ}=180-angle{AQP}-angle{MAQ}-ane{APQ}=angle{PAQ}-angle{MAQ}. Ainsi angle{MAQ}=1/2angle{PAQ} et ainsi AM est bissectrice de {PAQ}. Pour montre que PQ=1/2(AP+AQ) alors il suffit de remarquer qu'il existe une homothétie de centre A et valeur 3/4 qui renvoie (C) à (C') et ainsi renvoie P à R et Q àS ce qui donne AS=3/4AQ et AR=3/4AP. D'autre pat par la puissance de P et Q au cercle (C') nous avons : PM²=PR.PA=1/4AP² et de même QM²=1/4AQ² finalement : PQ=PM+PQ=1/2AP+1/2AQ=1/2(AP+AQ)
Sauf erreur  .. | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  Mer 24 Aoû 2011, 22:41 Mer 24 Aoû 2011, 22:41 | |
| pour le problème 3,pourriez vous me donner une idée sur l'utilité du a,b,c et d>1/2 ?!
et voici une autre solution:
on a : 4abcd>=4(a²+b²+c²+d²)>=(a+b+c+d)² (d'après cauchy schawrz)
donc il suffit de démontrer que:
(a+b+c+d)²>=4(a+b+c+d)-32
ce qui est évident car:
p²-4p+32 >=0 pour tout p de R vu que le dét. et inférieur à 0
donc: abcd>=a+b+c+d-8
CQFD
| |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) Sujet: Re: test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008)  | |
| |
|
  | |
| | test n°1 stage du rabat (25-29 /01/2008) (olympiade 2008) |  |
|
