| | inega pour collegien |  |
|
|
| Auteur | Message |
|---|
topmath
Expert sup
 Nombre de messages : 1266
Age : 31
Localisation : planète de mathematicien
Date d'inscription : 23/10/2007
| | Sujet: inega pour collegien Lun 17 Mar 2008, 13:19 | |
| | |
|
| | |
mathsmaster
Expert sup
Nombre de messages : 1500
Age : 31
Localisation : chez moi.
Date d'inscription : 06/02/2008
| | Sujet: Re: inega pour collegien Lun 17 Mar 2008, 13:21 | |
| mercie pour l'exo j vais y reflaichir | |
|
| | |
memath
Expert sup
Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
| |
| | |
topmath
Expert sup
Nombre de messages : 1266
Age : 31
Localisation : planète de mathematicien
Date d'inscription : 23/10/2007
| | Sujet: Re: inega pour collegien Lun 17 Mar 2008, 13:45 | |
| | |
|
| | |
red11
Expert sup
Nombre de messages : 674
Age : 31
Date d'inscription : 28/06/2007
| | Sujet: Re: inega pour collegien Lun 17 Mar 2008, 13:52 | |
| Salut,
(a-b)²+(b-c)²+(a-c)²>=0
2a²+2b²+2c²-2ab-2ac-2bc>=0
2a²+2b²+2c²>=2ab+2bc+2ac
3a²+3b²+3c²>=(a+b+c)²
3a²+3b²+3c²>=1
a²+b²+c²+1>=4/3
a²+b²+c²-2+3>=4/3
a²-2a+1+b²-2b+1+c²-2c+1>=4/3
(a-1)²+(b-1)²+(c-1)²>=4/3 | |
|
| | |
topmath
Expert sup
Nombre de messages : 1266
Age : 31
Localisation : planète de mathematicien
Date d'inscription : 23/10/2007
| | Sujet: Re: inega pour collegien Lun 17 Mar 2008, 14:00 | |
| - red11 a écrit:
- Salut,
(a-b)²+(b-c)²+(a-c)²>=0
2a²+2b²+2c²-2ab-2ac-2bc>=0
2a²+2b²+2c²>=2ab+2bc+2ac
3a²+3b²+3c²>=(a+b+c)²
3a²+3b²+3c²>=1
a²+b²+c²+1>=4/3
a²+b²+c²-2+3>=4/3
a²-2a+1+b²-2b+1+c²-2c+1>=4/3
(a-1)²+(b-1)²+(c-1)²>=4/3 wi c ça | |
|
| | |
memath
Expert sup
Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
| | Sujet: Re: inega pour collegien Lun 17 Mar 2008, 21:22 | |
| - red11 a écrit:
- Salut,
(a-b)²+(b-c)²+(a-c)²>=0
2a²+2b²+2c²-2ab-2ac-2bc>=0
2a²+2b²+2c²>=2ab+2bc+2ac
3a²+3b²+3c²>=(a+b+c)²
3a²+3b²+3c²>=1
a²+b²+c²+1>=4/3
a²+b²+c²-2+3>=4/3
a²-2a+1+b²-2b+1+c²-2c+1>=4/3
(a-1)²+(b-1)²+(c-1)²>=4/3 Bien joué  | |
|
| | |
memath
Expert sup
Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
| | Sujet: Re: inega pour collegien Lun 17 Mar 2008, 21:34 | |
| Autrement (c toujours meilleur d avoir plus qu une methode )  | |
|
| | |
lilass
Expert grade1
 Nombre de messages : 441
Age : 30
Localisation : voie lactée...
Date d'inscription : 01/01/2008
| | Sujet: Re: inega pour collegien Mar 18 Mar 2008, 21:28 | |
| - red11 a écrit:
- Salut,
(a-b)²+(b-c)²+(a-c)²>=0
2a²+2b²+2c²-2ab-2ac-2bc>=0
2a²+2b²+2c²>=2ab+2bc+2ac
3a²+3b²+3c²>=(a+b+c)²
3a²+3b²+3c²>=1
a²+b²+c²+1>=4/3
a²+b²+c²-2+3>=4/3
a²-2a+1+b²-2b+1+c²-2c+1>=4/3(a-1)²+(b-1)²+(c-1)²>=4/3 puis je savoir comment etes vous arrivé aux etapes ecrite en rouge  mrci d'avance | |
|
| | |
Perelman
Expert sup
Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
| | Sujet: Re: inega pour collegien Mar 18 Mar 2008, 21:46 | |
| voici: 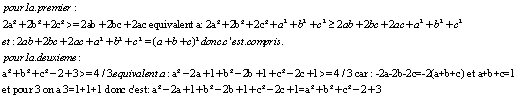 desole le premier ligne: c'est a^2+b^2+c^2 | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: inega pour collegien | |
| |
|
| | |
| | inega pour collegien | |
|
