| | exo arith |  |
|
+4raito321 mni hamzaaa y-a-ss-i-n-e 8 participants |
|
| Auteur | Message |
|---|
y-a-ss-i-n-e
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 33
Localisation : maroc
Date d'inscription : 21/12/2007
 |  Sujet: exo arith Sujet: exo arith  Lun 31 Mar 2008, 01:29 Lun 31 Mar 2008, 01:29 | |
| prouver que 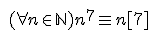 | |
|
  | |
hamzaaa
Expert sup

 Nombre de messages : 744 Nombre de messages : 744
Age : 37
Localisation : Montréal...
Date d'inscription : 15/11/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Lun 31 Mar 2008, 07:30 Lun 31 Mar 2008, 07:30 | |
| Une étude des cas, et peut être une calculette, et c'est bon lol
n=a[7] avec a=0,1...6. | |
|
  | |
y-a-ss-i-n-e
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 33
Localisation : maroc
Date d'inscription : 21/12/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Lun 31 Mar 2008, 10:45 Lun 31 Mar 2008, 10:45 | |
| merci hamza est ce c vrai  | |
|
  | |
mni
Maître

 Nombre de messages : 218 Nombre de messages : 218
Age : 33
Localisation : casa
Date d'inscription : 30/05/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mar 01 Avr 2008, 19:57 Mar 01 Avr 2008, 19:57 | |
| selon le theorème de fermat on a
x ^ n=1 et n premier ==>x°(n)equivaut x(n) | |
|
  | |
raito321
Expert grade1
 Nombre de messages : 427 Nombre de messages : 427
Age : 34
Localisation : Témara
Date d'inscription : 13/12/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mar 01 Avr 2008, 20:58 Mar 01 Avr 2008, 20:58 | |
| - y-a-ss-i-n-e a écrit:
- merci hamza
est ce c vrai
 Seulement pour n premier !! | |
|
  | |
nounoua
Expert grade2

 Nombre de messages : 338 Nombre de messages : 338
Age : 33
Date d'inscription : 18/11/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 11:44 Mer 02 Avr 2008, 11:44 | |
| | |
|
  | |
faussejoie
Expert grade1

 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : winouu
Date d'inscription : 15/08/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 12:37 Mer 02 Avr 2008, 12:37 | |
| vous etes deja en arithmetique | |
|
  | |
raito321
Expert grade1
 Nombre de messages : 427 Nombre de messages : 427
Age : 34
Localisation : Témara
Date d'inscription : 13/12/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:03 Mer 02 Avr 2008, 13:03 | |
| - nounoua a écrit:
- j'ai rien comprie
Y a un théorême qui dit (théorème de fermat) : si p est permier alors pour tout n dans IN on a : n^p=n[p] Pour le démontrer y a tout un exo : 1/ montrer pour tout k dans [|1,p-1|] p divise  2/ montrer que (n+1)^p = (n^p) + 1 [p] Et enfin déduire que n^p = n [p] et aussi n^{p-1}=1[p] | |
|
  | |
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:05 Mer 02 Avr 2008, 13:05 | |
| c est pas evident raito , car ils nont pas fait le théoreme de Gauss | |
|
  | |
faussejoie
Expert grade1

 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : winouu
Date d'inscription : 15/08/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:06 Mer 02 Avr 2008, 13:06 | |
| | |
|
  | |
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:10 Mer 02 Avr 2008, 13:10 | |
| | |
|
  | |
nounoua
Expert grade2

 Nombre de messages : 338 Nombre de messages : 338
Age : 33
Date d'inscription : 18/11/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:13 Mer 02 Avr 2008, 13:13 | |
| ce ke vous dite est plus ke notre niveau | |
|
  | |
raito321
Expert grade1
 Nombre de messages : 427 Nombre de messages : 427
Age : 34
Localisation : Témara
Date d'inscription : 13/12/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:13 Mer 02 Avr 2008, 13:13 | |
| Ben oui!!
Oui ils n'ont pas fais le théorême de GAUSS mais si on voit la série DIMADIMA y a plusieurs exo qui sont résolu grace à GAUSS !!
De plus comment démontrer Fermat sans Gauss ??!! | |
|
  | |
nounoua
Expert grade2

 Nombre de messages : 338 Nombre de messages : 338
Age : 33
Date d'inscription : 18/11/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:18 Mer 02 Avr 2008, 13:18 | |
| c'est pour cette raison j'ai ecrit j'ai pas comprie | |
|
  | |
raito321
Expert grade1
 Nombre de messages : 427 Nombre de messages : 427
Age : 34
Localisation : Témara
Date d'inscription : 13/12/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:20 Mer 02 Avr 2008, 13:20 | |
| Ici on a p=7 je pense qu'on peut le faire par recurence !! | |
|
  | |
nounoua
Expert grade2

 Nombre de messages : 338 Nombre de messages : 338
Age : 33
Date d'inscription : 18/11/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:26 Mer 02 Avr 2008, 13:26 | |
| tu pe me donner la solution complete | |
|
  | |
raito321
Expert grade1
 Nombre de messages : 427 Nombre de messages : 427
Age : 34
Localisation : Témara
Date d'inscription : 13/12/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:30 Mer 02 Avr 2008, 13:30 | |
| On a tjrs besoin du fait que 7 divise C^7_k!!
Je posterai la réponse plus tard !! | |
|
  | |
nounoua
Expert grade2

 Nombre de messages : 338 Nombre de messages : 338
Age : 33
Date d'inscription : 18/11/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:31 Mer 02 Avr 2008, 13:31 | |
| je ve slm savoir [7]=partie entiere !!!!!!!!!!
si c'est oui je trouve pas ke c logique | |
|
  | |
raito321
Expert grade1
 Nombre de messages : 427 Nombre de messages : 427
Age : 34
Localisation : Témara
Date d'inscription : 13/12/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:45 Mer 02 Avr 2008, 13:45 | |
| Non !!
C'est modulo !!
Si t'as pas fais arithmétique mtn ben ne te casse pas trop la tête !!
Par exemple a=bq+r alors a=r[b] et a-r=0[b] qui veut dire que b divise a-r | |
|
  | |
nounoua
Expert grade2

 Nombre de messages : 338 Nombre de messages : 338
Age : 33
Date d'inscription : 18/11/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:45 Mer 02 Avr 2008, 13:45 | |
| | |
|
  | |
faussejoie
Expert grade1

 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : winouu
Date d'inscription : 15/08/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:46 Mer 02 Avr 2008, 13:46 | |
| je crois que ns avons les arithmétiques cet an | |
|
  | |
raito321
Expert grade1
 Nombre de messages : 427 Nombre de messages : 427
Age : 34
Localisation : Témara
Date d'inscription : 13/12/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:47 Mer 02 Avr 2008, 13:47 | |
| | |
|
  | |
faussejoie
Expert grade1

 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : winouu
Date d'inscription : 15/08/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 13:49 Mer 02 Avr 2008, 13:49 | |
| | |
|
  | |
y-a-ss-i-n-e
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 33
Localisation : maroc
Date d'inscription : 21/12/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 16:28 Mer 02 Avr 2008, 16:28 | |
| - raito321 a écrit:
et aussi n^{p-1}=1[p] c vrai si n ^ p = 1 (^ :pgdc) | |
|
  | |
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: exo arith Sujet: Re: exo arith  Mer 02 Avr 2008, 19:57 Mer 02 Avr 2008, 19:57 | |
| voila pour la solution
traiter tous les cas simplement :
par exemple
n=1[7] =>n^7=1[7]
n=2[7] =>n^7=2[7]
......
......
......
en traitant tous les cas concluez! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: exo arith Sujet: Re: exo arith  | |
| |
|
  | |
| | exo arith |  |
|
