| | Défi pour les tronc commun |  |
|
|
| Auteur | Message |
|---|
Invité
Invité
 |  Sujet: Défi pour les tronc commun Sujet: Défi pour les tronc commun  Sam 19 Avr 2008, 12:32 Sam 19 Avr 2008, 12:32 | |
| Bonjour,  Trouvez n .  |
|
  | |
mathsmaster
Expert sup

 Nombre de messages : 1500 Nombre de messages : 1500
Age : 31
Localisation : chez moi.
Date d'inscription : 06/02/2008
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Sam 19 Avr 2008, 14:44 Sam 19 Avr 2008, 14:44 | |
| salut je crois qu'ils y a beucoup de valeurs de n et je crois que tu veut la plus petite d'entre eux.
si c le cas tu doit factoriser par 2^8 et puis tu cherche la plus petite valeurs de n. | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 14:14 Dim 20 Avr 2008, 14:14 | |
| | |
|
  | |
nounoua
Expert grade2

 Nombre de messages : 338 Nombre de messages : 338
Age : 33
Date d'inscription : 18/11/2007
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 14:42 Dim 20 Avr 2008, 14:42 | |
| | |
|
  | |
Invité
Invité
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 15:34 Dim 20 Avr 2008, 15:34 | |
| Quand je dis un défi c'est votre défi en réponse a h99 n n'est pas égale à 0
et à mathmaster et à nounoua n est plus grand que 10
donc qui a donné hmaro? |
|
  | |
Invité
Invité
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 15:36 Dim 20 Avr 2008, 15:36 | |
| |
|
  | |
nounoua
Expert grade2

 Nombre de messages : 338 Nombre de messages : 338
Age : 33
Date d'inscription : 18/11/2007
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 15:47 Dim 20 Avr 2008, 15:47 | |
| | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 16:05 Dim 20 Avr 2008, 16:05 | |
| | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 16:24 Dim 20 Avr 2008, 16:24 | |
| voila,j'espere que c'est vrai. 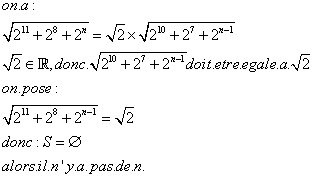 | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 16:30 Dim 20 Avr 2008, 16:30 | |
| PS: j'ai ecrit V(2^10+2^7+2^(n-1)) doit egale a V2 car puisque V2 appartient a IR donc V(2^10+2^7+2^(n-1)) doit egale a V2 pour que V2.V(2^10+2^7+2^(n-1)) appartient a IN
un nombre appartient a IR * nombre appartient a X=nombre appartient a IR
X: ensemble quelconque. | |
|
  | |
Invité
Invité
 |  Sujet: solution Sujet: solution  Dim 20 Avr 2008, 16:31 Dim 20 Avr 2008, 16:31 | |
| Cela équivaut à 2^11 +2^8 +2^n =a² donc 2^8 *9 +2^n=a² 2^n=a²-9*2^8 =(a-3*2^4)(a+3*2^4) a-3*2^4=2^p a+3*2^4=2^q telque p+q=n a=2^p +3*2^4=2^q-3*2^4 2^q -2^p=(3*2^4)+(3*2^5) (2^p)[2^(q-p)-1)]=3*2^5 selon le Théorème fondamental de l'arithmétique (une seule écriture possible produit de nombres premiers) 2^p=2^5 et 2^(q-p)-1=3 p=5 et 2^(q-p)=2² q-p=2 q-5=2 q=7 donc p=2 et q=7 sachant que n=p+q alors n=5+7=12 n=12 VERIFICATION 2^11 +2^8+2^12=2^8(2^3+1+2^4) =2^8(8+1+16) =2^8*25 =(2^4*5)²=80²   |
|
  | |
khatir123
Maître

 Nombre de messages : 190 Nombre de messages : 190
Age : 32
Date d'inscription : 05/03/2008
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 16:56 Dim 20 Avr 2008, 16:56 | |
| salut je m'adresse à h99 je crois qu'il n'y a pas que le cas de V(2^10+2^7+2^(n-1))=v2  @+ | |
|
  | |
mathsmaster
Expert sup

 Nombre de messages : 1500 Nombre de messages : 1500
Age : 31
Localisation : chez moi.
Date d'inscription : 06/02/2008
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  Dim 20 Avr 2008, 17:19 Dim 20 Avr 2008, 17:19 | |
| c'etait un exo difficile merci mon ami Moncefelmoumen  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Défi pour les tronc commun Sujet: Re: Défi pour les tronc commun  | |
| |
|
  | |
| | Défi pour les tronc commun |  |
|
