| | cauchy shwarz. |  |
|
|
| Auteur | Message |
|---|
red11
Expert sup

 Nombre de messages : 674 Nombre de messages : 674
Age : 31
Date d'inscription : 28/06/2007
 |  Sujet: cauchy shwarz. Sujet: cauchy shwarz.  Lun 23 Juin 2008, 18:26 Lun 23 Juin 2008, 18:26 | |
| Qui peut m'expliquer l'inégalité de cauchy-shwarz? | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  Lun 14 Juil 2008, 14:43 Lun 14 Juil 2008, 14:43 | |
| | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  Lun 14 Juil 2008, 14:49 Lun 14 Juil 2008, 14:49 | |
| - red11 a écrit:
- Qui peut m'expliquer l'inégalité de cauchy-shwarz?
BJR red11 !! Il suffit de faire un tour sur Wikipédia ICI : http://fr.wikipedia.org/wiki/In%C3%A9galit%C3%A9_de_Cauchy-Schwarz Tu y trouveras ton bonheur !! LHASSANE | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  Lun 14 Juil 2008, 17:37 Lun 14 Juil 2008, 17:37 | |
| slt l'inegalité de Caushy shwartz ; soit a_i et b_i des reels positifs avc i={1,2,3.....n} on a : ((a_1)²+(a_2)²+....+(a_n)²)((b_1)²+(b_2)²+....+(b_n)²) >= (a_1b_1+a_2b_2+....+a_n+b_n)² il y a aussi l interpretation geometrique qui existe dans le programme des tronc communs : soit , U et V deux vecteurs ||U||².||V||²>= (u.v)² la generalisation de l inegalité de caushy s apelle l inegalité de Holder , tu peux la chercher sur wiki  | |
|
  | |
red11
Expert sup

 Nombre de messages : 674 Nombre de messages : 674
Age : 31
Date d'inscription : 28/06/2007
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  Jeu 17 Juil 2008, 14:52 Jeu 17 Juil 2008, 14:52 | |
| - Oeil_de_Lynx a écrit:
- red11 a écrit:
- Qui peut m'expliquer l'inégalité de cauchy-shwarz?
BJR red11 !!
Il suffit de faire un tour sur Wikipédia ICI :
http://fr.wikipedia.org/wiki/In%C3%A9galit%C3%A9_de_Cauchy-Schwarz
Tu y trouveras ton bonheur !!
LHASSANE Merci bcp mais je comprend pas sigma.   Je vais essayer de chercher ce qu'elle veut dire(si vous avez des infos n'ésiter pas.) A+ | |
|
  | |
red11
Expert sup

 Nombre de messages : 674 Nombre de messages : 674
Age : 31
Date d'inscription : 28/06/2007
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  Jeu 17 Juil 2008, 14:53 Jeu 17 Juil 2008, 14:53 | |
| - memath a écrit:
- slt
l'inegalité de Caushy shwartz ;
soit a_i et b_i des reels positifs avc i={1,2,3.....n}
on a :
((a_1)²+(a_2)²+....+(a_n)²)((b_1)²+(b_2)²+....+(b_n)²) >= (a_1b_1+a_2b_2+....+a_n+b_n)²
il y a aussi l interpretation geometrique qui existe dans le programme des tronc communs :
soit , U et V deux vecteurs
||U||².||V||²>= (u.v)²
la generalisation de l inegalité de caushy s apelle l inegalité de Holder , tu peux la chercher sur wiki  Merci beaucoup memath trés interéssant .Mais je comprend pas ce que veut dire i.Je vais essayer de faire un ptit saut au court du TC peut étre que j'y trouverai une réponse.a _1 que veut dire ce trait?i={1,2,3.....n} wach ca veut dire i tantami ila IN? | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  Ven 18 Juil 2008, 15:26 Ven 18 Juil 2008, 15:26 | |
| - red11 a écrit:
- memath a écrit:
- slt
l'inegalité de Caushy shwartz ;
soit a_i et b_i des reels positifs avc i={1,2,3.....n}
on a :
((a_1)²+(a_2)²+....+(a_n)²)((b_1)²+(b_2)²+....+(b_n)²) >= (a_1b_1+a_2b_2+....+a_n+b_n)²
il y a aussi l interpretation geometrique qui existe dans le programme des tronc communs :
soit , U et V deux vecteurs
||U||².||V||²>= (u.v)²
la generalisation de l inegalité de caushy s apelle l inegalité de Holder , tu peux la chercher sur wiki  Merci beaucoup memath trés interéssant .Mais je comprend pas ce que veut dire i.Je vais essayer de faire un ptit saut au court du TC peut étre que j'y trouverai une réponse.a_1 que veut dire ce trait?i={1,2,3.....n} wach ca veut dire i tantami ila IN? je crois que i=(1,2,3....n) veut dire que i peut prendre tout ces nombres la , pas sur mais c ça ce que je croix . et pour le trait (_) je vais te le faire par image : 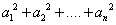 | |
|
  | |
red11
Expert sup

 Nombre de messages : 674 Nombre de messages : 674
Age : 31
Date d'inscription : 28/06/2007
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  Ven 18 Juil 2008, 18:28 Ven 18 Juil 2008, 18:28 | |
| | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  Sam 19 Juil 2008, 16:59 Sam 19 Juil 2008, 16:59 | |
| | |
|
  | |
boutheyna
Féru

 Nombre de messages : 45 Nombre de messages : 45
Age : 31
Localisation : fès
Date d'inscription : 21/04/2008
 | |
  | |
boutheyna
Féru

 Nombre de messages : 45 Nombre de messages : 45
Age : 31
Localisation : fès
Date d'inscription : 21/04/2008
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  Jeu 24 Juil 2008, 22:48 Jeu 24 Juil 2008, 22:48 | |
| il a raison et il a 16 ans en plus  joyeux annif  c'est le 24 juillet  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: cauchy shwarz. Sujet: Re: cauchy shwarz.  | |
| |
|
  | |
| | cauchy shwarz. |  |
|
