Exo d'aprés l'3aid !

sorry voila l'exo que je voulai poster: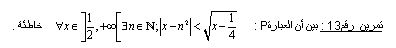

en fait cé 1exo de lancienne dimadima où on demande de montrer que la proposition est vraie?!

je m'excuse je vais essayer pour l'autre

dangerous mind a écrit:

pour la montrer on a n>=p si p= 90 donc la relation est vraie .
la negation :
(pour tout "p" appartient a N) (il y a "n" de N) telle que n <= p ==> 10>= (racine de) n

tu n'as pas fais attention aux >= et <

BSr
cé un bon exo a faire !?

oui..t'as raison Mr madani ...

je crois qu'on va utiliser la négation...

oui t'as raison Koutaiba on va user la négation

J'aimerai bien voir comment dangerous mind et koutaiba toute la démonstration.

Salut à tous,

on a : x-n² < V(x-1/4)
<=> (x-n²)² < x-1/4
<=> x² - (2n²+1) x + 1/4 < 0
delta = 4n²+4n+1-4n^4 - 1
delta = 4(n²+n-n^4)
déjà si n²+n-n^4 < 0 on aura x² - (2n²+1) x + 1/4 > 0 (contradiction), et si n²+n-n^4 = 0 l'équation : x² - (2n²+1) x + 1/4 = 0 aura une solution , ce qui contredit l'inéquation, donc : n²+n-n^4 > 0 , et puisque n est un entier naturel , n=1 est la seule solution de l'inéquation
donc si la proposition est vraie, il existe le n=1 qui vérifie, mais si on remplace n par 1 dans l'inéquation de départ on trouve que x²+3x+5/4<0 ce qui est impossible, c juste sauf si -5/2<x<-1/2 or x est déjà plus grand que 1/2.
Finalement, la proposition est fausse.

Chessmaster a écrit:

Salut à tous,

on a : x-n² < V(x-1/4)
<=> (x-n²)² < x-1/4
<=> x² - (2n²+1) x + 1/4 < 0
delta = 4n²+4n+1-4n^4 - 1
delta = 4(n²+n-n^4)
déjà si n²+n-n^4 < 0 on aura x² - (2n²+1) x + 1/4 > 0 (contradiction), et si n²+n-n^4 = 0 l'équation : x² - (2n²+1) x + 1/4 = 0 aura une solution , ce qui contredit l'inéquation, donc : n²+n-n^4 > 0 , et puisque n est un entier naturel , n=1 est la seule solution de l'inéquation
donc si la proposition est vraie, il existe le n=1 qui vérifie, mais si on remplace n par 1 dans l'inéquation de départ on trouve que x²+3x+5/4<0 ce qui est impossible, c juste sauf si -5/2<x<-1/2 or x est déjà plus grand que 1/2.
Finalement, la proposition est fausse.

bsr
cé la méthode mais tu devrais rectifier l'erreur de frappe et discuter si delta est <0 ou >0 suivant les valeurs de n!!!

ça serait de dire que delta<0 ou =0 aboutit à une contradiction, et n=1 lorsque delta > 0

Chessmaster a écrit:

Salut à tous,

on a : x-n² < V(x-1/4)
<=> (x-n²)² < x-1/4
<=> x² - (2n²+1) x + 1/4 < 0
delta = 4n²+4n+1-4n^4 - 1
delta = 4(n²+n-n^4)
déjà si n²+n-n^4 < 0 on aura x² - (2n²+1) x + 1/4 > 0 (contradiction), et si n²+n-n^4 = 0 l'équation : x² - (2n²+1) x + 1/4 = 0 aura une solution , ce qui contredit l'inéquation, donc : n²+n-n^4 > 0 , et puisque n est un entier naturel , n=1 est la seule solution de l'inéquation
donc si la proposition est vraie, il existe le n=1 qui vérifie, mais si on remplace n par 1 dans l'inéquation de départ on trouve que x²+3x+5/4<0 ce qui est impossible, c juste sauf si -5/2<x<-1/2 or x est déjà plus grand que 1/2.
Finalement, la proposition est fausse.

salut ...
je crois qu'il y a une faute ...
on a
|x-n^2| < V(x-1/4)
(x-n²)² < x-1/4
x^2 + n^4 - 2 n^2 x < x - 1/4
x^2 - 2 n^2 x - x + n^4 + 1/4 < 0
x² - (2n²+1) x + n^4+ 1/4 < 0
DELTA = (2n²+1)^2 - 4(n^4+ 1/4)
= 4n^4 + 1 + 4n^2 - 4n^4 - 1
= 4 n^2
alors
DELTA > 0
donc
A x appartient à [1/2،+00[ : x² - (2n²+1) x + n^4+ 1/4 > 0
contradiction avec
x² - (2n²+1) x + n^4+ 1/4 < 0
alors
P est fausse

Effectivement, merci pour la correction =)

Koutaiba a écrit:

Chessmaster a écrit:

Salut à tous,

on a : x-n² < V(x-1/4)
<=> (x-n²)² < x-1/4
<=> x² - (2n²+1) x + 1/4 < 0
delta = 4n²+4n+1-4n^4 - 1
delta = 4(n²+n-n^4)
déjà si n²+n-n^4 < 0 on aura x² - (2n²+1) x + 1/4 > 0 (contradiction), et si n²+n-n^4 = 0 l'équation : x² - (2n²+1) x + 1/4 = 0 aura une solution , ce qui contredit l'inéquation, donc : n²+n-n^4 > 0 , et puisque n est un entier naturel , n=1 est la seule solution de l'inéquation
donc si la proposition est vraie, il existe le n=1 qui vérifie, mais si on remplace n par 1 dans l'inéquation de départ on trouve que x²+3x+5/4<0 ce qui est impossible, c juste sauf si -5/2<x<-1/2 or x est déjà plus grand que 1/2.
Finalement, la proposition est fausse.

salut ...
je crois qu'il y a une faute ...
on a
|x-n^2| < V(x-1/4)
(x-n²)² < x-1/4
x^2 + n^4 - 2 n^2 x < x - 1/4
x^2 - 2 n^2 x - x + n^4 + 1/4 < 0
x² - (2n²+1) x + n^4+ 1/4 < 0
DELTA = (2n²+1)^2 - 4(n^4+ 1/4)
= 4n^4 + 1 + 4n^2 - 4n^4 - 1
= 4 n^2
alors
DELTA > 0
donc
A x appartient à [1/2،+00[ : x² - (2n²+1) x + n^4+ 1/4 > 0
contradiction avec
x² - (2n²+1) x + n^4+ 1/4 < 0
alors
P est fausse

bsr
le début de la démarche est bon mais aprés il y a une grave erreur logique du fait qu'on a inversé le role de l'inconnu qui est n et le doné qui est x!?

madani a écrit:

Koutaiba a écrit:

Chessmaster a écrit:

Salut à tous,

on a : x-n² < V(x-1/4)
<=> (x-n²)² < x-1/4
<=> x² - (2n²+1) x + 1/4 < 0
delta = 4n²+4n+1-4n^4 - 1
delta = 4(n²+n-n^4)
déjà si n²+n-n^4 < 0 on aura x² - (2n²+1) x + 1/4 > 0 (contradiction), et si n²+n-n^4 = 0 l'équation : x² - (2n²+1) x + 1/4 = 0 aura une solution , ce qui contredit l'inéquation, donc : n²+n-n^4 > 0 , et puisque n est un entier naturel , n=1 est la seule solution de l'inéquation
donc si la proposition est vraie, il existe le n=1 qui vérifie, mais si on remplace n par 1 dans l'inéquation de départ on trouve que x²+3x+5/4<0 ce qui est impossible, c juste sauf si -5/2<x<-1/2 or x est déjà plus grand que 1/2.
Finalement, la proposition est fausse.

salut ...
je crois qu'il y a une faute ...
on a
|x-n^2| < V(x-1/4)
(x-n²)² < x-1/4
x^2 + n^4 - 2 n^2 x < x - 1/4
x^2 - 2 n^2 x - x + n^4 + 1/4 < 0
x² - (2n²+1) x + n^4+ 1/4 < 0
DELTA = (2n²+1)^2 - 4(n^4+ 1/4)
= 4n^4 + 1 + 4n^2 - 4n^4 - 1
= 4 n^2
alors
DELTA > 0
donc
A x appartient à [1/2،+00[ : x² - (2n²+1) x + n^4+ 1/4 > 0
contradiction avec
x² - (2n²+1) x + n^4+ 1/4 < 0
alors
P est fausse

bsr
le début de la démarche est bon mais aprés il y a une grave erreur logique du fait qu'on a inversé le role de l'inconnu qui est n et le doné qui est x!?

Salut Mr madani ...

au début merci pour la correction ..

alors il faut que l'équation soit comme ça :
x^2 - 2 n^2 x - x + n^4 + 1/4 < 0
n^4 - 2 x n^2 + x^2 - x + 1/4 < 0
mais j'ai pas bien compris la raison de cette méthode ..

pour démontrer qu'il n'existe aucun n qui vérifie cette inéquation sachant qu'elle est vraie pour n'importe quel x appartient à ]1/2;+inf[

Chessmaster a écrit:

pour démontrer qu'il n'existe aucun n qui vérifie cette inéquation sachant qu'elle est vraie pour n'importe quel x appartient à ]1/2;+inf[

en effet il faut determiner au moins un x pour le quel le n n'existe pas?!!

Oui, mais moi j'ai voulu démontrer plus fort que c'est pour tout x, je sais que ce n'est pas nécessaire, sinon il faut choisir une seule valeur de x et dire que la négation de cette proposition est vraie d'où le résultat.

Chessmaster a écrit:

Oui, mais moi j'ai voulu démontrer plus fort que c'est pour tout x, je sais que ce n'est pas nécessaire, sinon il faut choisir une seule valeur de x et dire que la négation de cette proposition est vraie d'où le résultat.

pour ttes x tu ne peux ps ! et ce qui est faux ici et d'ailleurs ds tt ex contenant le quantificateur qq soit!

Oui finalement j'avais fait une faute dans la rédaction de la démonstration.

Chessmaster a écrit:

sinon il faut choisir une seule valeur de x et dire que la négation de cette proposition est vraie d'où le résultat.

Chessmaster a écrit:

Oui finalement j'avais fait une faute dans la rédaction de la démonstration.

Chessmaster a écrit:

sinon il faut choisir une seule valeur de x et dire que la négation de cette proposition est vraie d'où le résultat.

le pb cé de le trouver et pour cela il faut resoudre l' inequation que tu as trouvé avt!!!

bof c'est simple :
quand on veux démontrer la négation FAUSSE : (il existe x pour tout n)
l'équation <==> n^4 -2xn²+x²-x+1/4>0
delta = 4x-1
pour que : n^4 -2xn²+x²-x+1/4>0 soit vraie pour tout n il faut que delta soit négatif strictement donc 4x-1<0 donc x<1/4 or x>1/2 donc il n'existe pas de x pour tout n, la négation est fausse , d'où la proposition est vraie
Effectivement il y avait une faute dans l'énoncé parce que j'ai vu mon ancien dima dima où on nous demande de la démontrer à savoir qu'elle est vraie non pas fausse.

Chessmaster a écrit:

bof c'est simple :
quand on veux démontrer la négation FAUSSE : (il existe x pour tout n)
l'équation <==> n^4 -2xn²+x²-x+1/4>0
delta = 4x-1
pour que : n^4 -2xn²+x²-x+1/4>0 soit vraie pour tout n il faut que delta soit négatif strictement donc 4x-1<0 donc x<1/4 or x>1/2 donc il n'existe pas de x pour tout n, la négation est fausse , d'où la proposition est vraie
Effectivement il y avait une faute dans l'énoncé parce que j'ai vu mon ancien dima dima où on nous demande de la démontrer à savoir qu'elle est vraie non pas fausse.

termines ton raisonnement car n est ds N et nn ds R!

de IN ou de R ça change rien et pour R c'est plus général