equation

montrer que l'equation: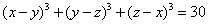


n'admet pas de solution dans Z.

bonne chance!!

on sait que pour tout a,b et c on a :
a^3+b^3+c^3 = 1/2(a+b+c)[(a-b)²+(b-c)²+(c-a)²] + 3abc
a^3+b^3+b^3
=1/2 (x-y+y-z+z-x)[...] + 3(x-y)(y-z)(z-x)
=3(x-y)(y-z)(z-x) = 30
donc (x-y)(y-z)(z-x)=10
(x-y)(yz-xy-z²+xz)=10
xyz-x²y-xz²+x²z-y²z+xy²+yz²-xyz=10
x²y-xz²+x²z-y²z+xy²+yz²=10
x²(y-z)+y²(x-z)+z²(y-x)=10
...
on a aussi : z=<x ou x=<y

tu peux svp completer la solution?

je ne sais pas comment continuer c'était juste une idée =)

on peut demontrer par absurde.

c'est plus facile, non?

Oui je pense que ça serait plus efficace

tu peux m'expliquer chessmaster le passage:

a^3+b^3+c^3 = 1/2(a+b+c)[(a-b)²+(b-c)²+(c-a)²] + 3abc
a^3+b^3+b^3
=1/2 (x-y+y-z+z-x)[...] + 3(x-y)(y-z)(z-x)
=3(x-y)(y-z)(z-x) = 30

merci d'avance.

a^3+b^3+c^3 = 1/2(a+b+c)[(a-b)²+(b-c)²+(c-a)²] + 3abc
ça tu peux le vérifier en développant l'expression de droite, donc en posant : a=x-y, b =y-z et c=z-x on aura :
(x-y)^3+(y-z)^3+(z-x)^3 = 1/2 (x-y+y-z+z-x)[(x-2y+z)²+(y-2z+x)²+(z-2x+y)²] + 3(x-y)(y-z)(z-x)
=0 + 3(x-y)(y-z)(z-x) = 3(x-y)(y-z)(z-x)

ok merci.

sinon la suite :
(x-y)(y-z)(z-x)=10 = 1.2.5
x-y=1 si on additionne les 3 équations on aura : 0=8 (faux)
y-z=2
z-x=5
prends les dans n'importe quel ordre, met -1 -2 -5 à la place là où tu veux ça sera toujours une contradiction en additionnant les 3 équations car 0#+/-1 +/-2 +/-5

mais nous on veux demontrer qu'il n'existe pas de x,y,z dans Z

mais toi mon pote t'as pas cite que x,y,z ne peuvent pas appartenir a Z.

le fait d'avoir : (x-y)(y-z)(z-x)=10 = 1.2.5 et de dire que :
x-y=+/-1
y-z=+/-2
z-x=+/-5
c'est qu'on a déjà supposé qu'il appartenait à Z (démonstration par l'absurde) parce que s'ils étaient dans R, je n'aurais pas le droit de dire un truc pareil

ok c'est bon.

Salu les amiss ! j trouvé la réponse !!
A la fin on trouve ke (x-y)(y-z)(z-x)=10
Ce ki ve dire : x-y>0 et y-z>0 et z-x>0 psk 10>0
c a dire ke : x>y>z et z>x
Wa hada tana9oud !! Donc l hypothése kon a fé au départ été fausse ! c a dire ke X et y et Z N apprt po a Z !

c'est tres bon joué Anaslematheux.

salut les gars! j'ai le meme exo à rendre le lundi. la méthode que vous avez utiliser est bien sauf que j'ai po bien compris le passage:
a^3+b^3+c^3= [ (a+b)(a²-ab+b²) + (a+c)(a²-ac+c²) + (b+c)(b²-bc+b²)]/2
pourriez vous le démontrer en oubliant la méthode du '' développe [ (a+b)(a²-ab+b²) + (a+c)(a²-ac+c²) + (b+c)(b²-bc+b²)]/2 et tu aura la réponse''
je veux dire qlqun peut il démontrer cette égalité en partant de a^3+b^3+c^3
merci d'avance!!

developper le cote droit et tu vas arriver au cote gauche.

slt tt le monde, je suis nouveau sur ce forum , donc j'espère que mes contributions seront les bienvenues
voilà, je propose une methode pour cet exo :
supposons que l''equation citée admet un triplet de solutions dans Z. Nous savons que pour tout (a,b,c ) de Z*Z*Z : a+b+c = 0 implique que a^+b^3+c^3 = 3abc. (facile à démontrer )
en utlisant cette formule, et avec ( x-y ) + ( y-z ) + ( z-x ) = 0 on obtient : 3 (x-y)(y-z)(z-x) = 30.
posons mnt a=x-y , b = y -z et c = z-x, nous remarquons que a +b = -c , d'où : ab(a+b)= -10 et puisque ab at a+b appartiennent à Z : ( ab = 10 et a+b= -1 ) ou ( ab = 5 et a+b = -2 ) ou ( ab = 2 et a+b = -5 ) ou encore ( ab = 1 et a+b = -10 )
puis on résoud chaque système , on obtient à chaque fois des résultats qui n'appartiennent pas à Z, ce qui est contradictoire avec la supposition, donc et par absurde, cette equation n'admet pas de solutions entières. ( sauf erreur )
voilà, merci !

c juste mé faudrai savoir qu'on a po a+b+c=0
donc faudrai penser à autre chose

bah si, puisque ( x- y ) + ( y - z ) + ( z-x ) = 0
donc en principe on a : ( x-y)^3 + (y-z)^3 + (z-x)^3 = 3 (x-y)(y-z)(z-x) = 30, non ?

Anaslematheux a écrit:

Salu les amiss ! j trouvé la réponse !!
A la fin on trouve ke (x-y)(y-z)(z-x)=10
Ce ki ve dire : x-y>0 et y-z>0 et z-x>0 psk 10>0
c a dire ke : x>y>z et z>x
Wa hada tana9oud !! Donc l hypothése kon a fé au départ été fausse ! c a dire ke X et y et Z N apprt po a Z !

bah dabord on peut pas faire le pas que tu as fait car pour tt a,b et c
a*b*c>0 ne veut forcément dire que a>0 et b>0 et c>0 on peut même trouver que a<0 et c<0 et b>0 et toujour on n'obtient le produit supérieur à 0.
Donc ta méthode n'est pas logique et en plus que ça on a rien hypothéquer au début c'était pour tt x et y et z

exact, on aura donc soit:
- x-y>0 et y-z>0 et z-x>0
- x-y>0 et (y-z) et (z-x) négatifs
- (x-y) et (y-z) négatifs et z-x positif
- (x-y) et (z-x) négatifs et y-z positif
et en utilisant le truc de ''fassl alhalat'' on aura certainement une contradiction dans les quatres cas, ce qui veut dire que les solutions de cette équations n'appartiennent po à z!!!