nmo
Expert sup
 Nombre de messages : 2249
Age : 30
Localisation : Elgara
Date d'inscription : 29/10/2009
 | | Sujet: Minimum: Jeu 25 Juin 2015, 09:34 | |
| Quel est le minimum de la fonction =\sqrt{(x-6)^2+25}+\sqrt{(x+6)^2+121}) ? Bonne chance.
Dernière édition par nmo le Sam 01 Déc 2018, 10:38, édité 1 fois (Raison : Erreur de frappe) | |
|
aymanemaysae
Expert grade1
Nombre de messages : 428
Age : 27
Date d'inscription : 22/01/2014
| | Sujet: Re: Minimum: Lun 13 Juil 2015, 10:17 | |
| | |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 30
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Minimum: Sam 01 Déc 2018, 11:00 | |
| La solution de aymanemaysae est correcte. Sinon, on peut répondre à la question en utilisant l'inégalité de Minkowski:  : \sqrt{a^2+b^2}+\sqrt{c^2+d^2}\ge \sqrt{(a+c)^2+(b+d)^2}) avec égalité si et seulement si il existe 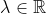 tel que 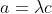 et 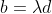 . Avec 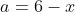 , 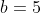 , 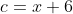 et 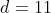 , on trouve  \ge \sqrt{12^2+16^2} = \sqrt{20^2} = 20) . Avec égalité si et seulement si il existe 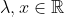 tel que ) et 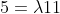 . La résolution de ce système donne 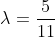 et 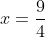 . En conclusion, on a:  : f(x) \ge f\left(\frac{9}{4}\right) = 20) . Sauf erreurs. | |
|
elhor_abdelali
Expert grade1
Nombre de messages : 489
Age : 61
Localisation : Maroc.
Date d'inscription : 24/01/2006
| | Sujet: Re: Minimum: Sam 27 Mar 2021, 02:56 | |
|  Dans le plan affine euclidien muni d'un repère orthonormé, considérons les points A(6,5) , B(-6,11) et B'(-6,-11) Si X(x,0) est un point mobile sur l'axe des abscisses, il est facile de voir que f(x) = AX + BX et comme BX = B'X , il n'est pas difficile de voir que le point de l'axe des abscisses qui réalise le minimum de f(x) = AX + B'X n'est autre que le point H intersection avec l'axe des abscisses de la droite (AB') qui a pour équation y = (4/3)x - 3 c'est à dire le point H(9/4,0) , et le minimum cherché est alors min f(x) = AB' = 20  sauf erreur bien entendu | |
|
