| | Un système: |  |
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Un système: Sujet: Un système:  Sam 28 Aoû 2010, 18:20 Sam 28 Aoû 2010, 18:20 | |
| Je vous présente cet exercice tiré de http://www.maths-express.com/olympiades/exercices_2.php. Soient m, n, et p trois nombres réels positifs tels que 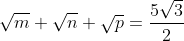 . Démontrez que le système suivant admet une solution unique: 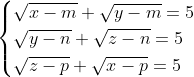 . Bonne chance.P.S: j'ai posté cet exercice car je ne sais pas la réponse. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Sam 28 Aoû 2010, 18:23 Sam 28 Aoû 2010, 18:23 | |
| Résolvez aussi en IR² ce système: \begin{cases}x^2+y^2=10\\x^3y+x^2y^2+xy^3=39\end{cases}) . Bonne chance. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Sam 28 Aoû 2010, 18:27 Sam 28 Aoû 2010, 18:27 | |
| - nmo a écrit:
- Résolvez aussi en IR² ce système:
\begin{cases}x^2+y^2=10\\x^3y+x^2y^2+xy^3=39\end{cases}) . .
Bonne chance. Permettez-moi de vous donner une petite idée en spoiler parce que le système est trivial. - Spoiler:
la deuxième équation équivaut à xy(x²+y²)+(xy)²=39 <=> 10xy+(xy)²-39=0 qui est assez simple
Bon jeu  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Sam 28 Aoû 2010, 18:42 Sam 28 Aoû 2010, 18:42 | |
| - nmo a écrit:
- Je vous présente cet exercice tiré de http://www.maths-express.com/olympiades/exercices_2.php.
Soient m, n, et p trois nombres réels positifs tels que 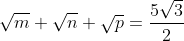 . .
Démontrez que le système suivant admet une solution unique:
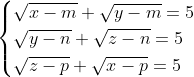 . .
Bonne chance.
P.S: j'ai posté cet exercice car je ne sais pas la réponse. Idée fondamentale : Soit (x,y) de IR² tel que x²+y²=1. Il existe un réel theta unique à 2PI près tel que (x,y)=(cos theta, sin theta). EDIT : Il faut creuser un peu plus. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Sam 28 Aoû 2010, 23:19 Sam 28 Aoû 2010, 23:19 | |
| Ma Solution du Probléme 1: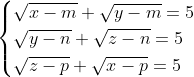 Lemme: Lemme: (De M.Marjani) Soit (x,y) des réels positives tel que 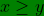 . On a 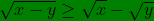 Démo: Démo:- Spoiler:
V(x-y) >= V(x) - V(y) <=> x-y >= x+y-2V(xy) <=> V(xy) >= y Ce qui est juste car x>y.
Puisqu'on a ces conditions, alors on peut façilement déduire que: 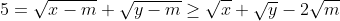 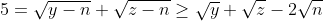 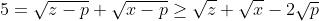 En sommant ces inégalités: -2\left ( \sqrt{m}+\sqrt{n}+\sqrt{p} \right )) Et alors: }{2}=\left ( \right \sqrt{m}+\sqrt{n}+\sqrt{p})+\frac{5}{2}) ====> (1) ====> (1)Et puisque 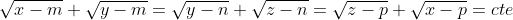 Alors ils ont le méme minumum, on déduit que: 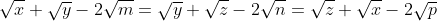 De ces égalités, on peut crée un petit systéme de trois equations, aprés sa résolution on trouve que 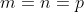 On déduit que 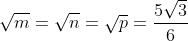 Alors il suffit de résoudrece systéme de 3 équations et 3 inconnus:  De la méme façon qu'on fait au dernier systéme, on aura 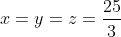 Qui est l'unique couple solution. Et (1) le confirme.  | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Dim 29 Aoû 2010, 03:31 Dim 29 Aoû 2010, 03:31 | |
| voici ma petite solution pour le 2eme système: on a: x²+y²=10 et x^3+x²y²+y^3=39 x²+y²=10 et x²y²+10xy-39=0 <=> xy=3 d'ou l'on déduit que : (x+y)²=16 alors:x+y=4 ou x+y=-4 le système devient alors: x+y=4 et xy=3 ou x+y=-4 et xy=3 ce qui nous mène aux équations suivantes: X²-4X+3=0 ou X²+4X+3=0 D'ou le résultat: x=1 et y=3 ou x=3 et y=1 en espérant que ça soit correcte! Ps:si quelqu'un pouvais me filer un tuyau pour apprendre a utiliser Latex, ça serait trop bien!  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Lun 30 Aoû 2010, 17:57 Lun 30 Aoû 2010, 17:57 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Lun 30 Aoû 2010, 18:05 Lun 30 Aoû 2010, 18:05 | |
| - W.Elluizi a écrit:
- voici ma petite solution pour le 2eme système:
on a:
x²+y²=10 et x^3+x²y²+y^3=39
x²+y²=10 et x²y²+10xy-39=0 <=> xy=3
d'ou l'on déduit que : (x+y)²=16
alors:x+y=4 ou x+y=-4
le système devient alors:
x+y=4 et xy=3 ou x+y=-4 et xy=3
ce qui nous mène aux équations suivantes:
X²-4X+3=0 ou X²+4X+3=0
D'ou le résultat: x=1 et y=3 ou x=3 et y=1
en espérant que ça soit correcte!
Ps:si quelqu'un pouvais me filer un tuyau pour apprendre a utiliser Latex, ça serait trop bien!  D'aprè ce qui est en rouge: On a x²y²+10xy-39=0. Donc (xy)²+10xy+25-64=0. Donc (xy+5)²-8²=0. Donc (xy+5-8 )(xy+5+8 )=0. Donc (xy-3)(xy+13)=0. Donc xy-3=0 ou xy+13=0. Donc xy=3 ou xy=-13. Il te reste un cas, alors. Pour l'autre, tu voulais dire x=-3 et y=-1. Au présent, tu as trouvé S={(1,3),(3,1),(-1,-3),(-3,-1)}. | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Lun 30 Aoû 2010, 18:10 Lun 30 Aoû 2010, 18:10 | |
| C'est exact, mais j'ai ignoré le 2ème cas car il ne vérifie point la 2ème équation! | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Mar 31 Aoû 2010, 13:29 Mar 31 Aoû 2010, 13:29 | |
| - nmo a écrit:
Les passages en rouges sont érroné.
Je te donne l'exemple suivant
On a 3>=1 et 3>=2.
Selon toi, on doit avoir 1=2 ce qui est faux.
Pour la première ligne en rouge, tu dis multiplier le côté gauche par 3.
Essaie encore une fois. Bon j'essaye d'expliquer: La premiére ligne en rouge, qu'une faute de frappe, le 1 du 15 n'était pas saisie, ce qui suit est juste.  Pour la deuxiéme remarque: Il s'agit d'une formule stable géneraliser qu'on a appliqué sur les LHS qui sont égales. C'est la méme chose que l'IAG. Et la complexité de ces trois nombres l'assure. (l'exemple que t'as donnée est trivial. Tu me donnes 3>2 et 3>1 ce qui est n'est pas le cas de notre EX >=) Si vous n'étes pas convaincu, j'avais une autre methode pour trouver que m=n=p ^_^ Une fois démontrer çelà tout devient façile. Lemme: (De M.Marjani) Soit (x,y) des réels positives tel que x>=m et y>=m. On a V(x-m)-V(y-m) =< V(x)-V(y)+V(m)Démo: - Spoiler:
V(x-m)=<V(x) donc il suffit de prouver que -V(y-m)=<-(V(y)-V(m)) ce qui est juste par lemme (1).
De méme: V(y-n)-V(z-n) =< V(y)-V(z)+V(n)V(z-p)-V(x-p) =< V(z)-V(x)+V(p) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Mar 14 Sep 2010, 17:44 Mar 14 Sep 2010, 17:44 | |
| - Dijkschneier a écrit:
- nmo a écrit:
- Je vous présente cet exercice tiré de http://www.maths-express.com/olympiades/exercices_2.php.
Soient m, n, et p trois nombres réels positifs tels que 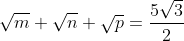 . .
Démontrez que le système suivant admet une solution unique:
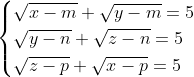 . .
Bonne chance.
P.S: j'ai posté cet exercice car je ne sais pas la réponse. Idée fondamentale : Soit (x,y) de IR² tel que x²+y²=1. Il existe un réel theta unique à 2PI près tel que (x,y)=(cos theta, sin theta).
EDIT : Il faut creuser un peu plus. Quel est l'intérêt de ce que tu viens de dire. Je vois qu'il n'a pas de relation avec l'exercice. | |
|
  | |
lamperouge
Maître

 Nombre de messages : 133 Nombre de messages : 133
Age : 28
Localisation : Casablanca
Date d'inscription : 13/01/2012
 |  Sujet: Re: Un système: Sujet: Re: Un système:  Dim 29 Jan 2012, 22:00 Dim 29 Jan 2012, 22:00 | |
| voici ma petite solution au 2eme exo
x²+y²=10 (1)
x^3y+x²y²+xy^3=39 (2)
(2)=> xy(x²+y²)+(xy)²-39=0
=> (xy)²+10xy-39=0
=> xy=3 ou xy=-13
mais le 2eme cas ne verifie po la 2eme equatiion
d'ou xy=3
(1)=>(x+y)²-2xy=10 et (x-y)²+2xy=10
=>(x+y)²=16 et (x-y)²=4
=>x+y=(+ou-)4 et x-y=(+ou-)2 et xy=3
=>(x=1 et y=3) ou (x=3 et y=1)
| |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Un système: Sujet: Re: Un système:  | |
| |
|
  | |
| | Un système: |  |
|
