| | ex logique!!! |  |
|
|
|
| Auteur | Message |
|---|
MARAM
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 32
Localisation : MOHAMMEDIA
Date d'inscription : 06/11/2008
 |  Sujet: ex logique!!! Sujet: ex logique!!!  Ven 07 Nov 2008, 22:49 Ven 07 Nov 2008, 22:49 | |
| SALUT TOUS
hola fi IR :
E(x²)=E(x)² | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Ven 07 Nov 2008, 22:50 Ven 07 Nov 2008, 22:50 | |
| | |
|
  | |
MARAM
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 32
Localisation : MOHAMMEDIA
Date d'inscription : 06/11/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Ven 07 Nov 2008, 22:52 Ven 07 Nov 2008, 22:52 | |
| E(x²) c.à.d. la partit entire de x² | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Ven 07 Nov 2008, 23:02 Ven 07 Nov 2008, 23:02 | |
| je pense que c'est:
S= Z U ]0, 1[. non? | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Ven 07 Nov 2008, 23:04 Ven 07 Nov 2008, 23:04 | |
| | |
|
  | |
MARAM
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 32
Localisation : MOHAMMEDIA
Date d'inscription : 06/11/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Ven 07 Nov 2008, 23:14 Ven 07 Nov 2008, 23:14 | |
| c est ce que je pense moi aussi
mais ton justification ???????? | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Ven 07 Nov 2008, 23:19 Ven 07 Nov 2008, 23:19 | |
| c'est simple à demontrer mais je crois pas qu'il est juste car si on prenant x= 1, 1 ou x= 1,2 ca verifie l'egalite!!!!!!!!!! | |
|
  | |
MARAM
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 32
Localisation : MOHAMMEDIA
Date d'inscription : 06/11/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Ven 07 Nov 2008, 23:53 Ven 07 Nov 2008, 23:53 | |
| non c' est juste
car qlq soit x/ 0<x<1
ON a 0<x²<1 | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Ven 07 Nov 2008, 23:55 Ven 07 Nov 2008, 23:55 | |
| non pas dans tt les cas.
j'ai trouve la soluce att un peu svp je vais la poster. | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 00:00 Sam 08 Nov 2008, 00:00 | |
| voila  :  | |
|
  | |
MARAM
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 32
Localisation : MOHAMMEDIA
Date d'inscription : 06/11/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 00:02 Sam 08 Nov 2008, 00:02 | |
| | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 00:04 Sam 08 Nov 2008, 00:04 | |
| pas de quoi  | |
|
  | |
mhdi
Expert sup
 Nombre de messages : 541 Nombre de messages : 541
Age : 32
Localisation : Tetouan
Date d'inscription : 21/11/2007
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 11:41 Sam 08 Nov 2008, 11:41 | |
| La solution de h99 est fausse(enfin, je pense ^^)
Voici la mienne :
Il est évident que Ax£Z : E(x²)=E(x)²
=> Z £ S
Supposons que x £ R\Z
=> x=p+r(p£Z et 0<r<1) =>E(x)²=p²
=> x²=p²+2pr+r² => E(x²)=p²+E(2pr+r²)
Donc, (E(x²)=E(x)² => p²+E(2pr+r²)=p²)
=>E(r²+2pr)=0 =>0=<r²+2pr<1
=>0=<r(r+2p) et r²+2pr<1
Puisque 0<r, -1/2<r/2=<p et r²+2pr<1
p£Z, donc 0=<p et r²+2pr<1
=>0=<p et (p+r)²<p²+1
=>p+r<V(p²+1)
=>p<x<V(p²+1)
=>A={x£R/ p<x<V(p²+1); p£N}UZ £ S
Finalement, on s'assure que Ax£A l'équation est vérifiée. Et on déduit que S=A | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 12:08 Sam 08 Nov 2008, 12:08 | |
| je sais pas si ta reponse est juste, car on n'a pas fait la partie entiere!!!, donc j'ai répondu d'apres ce que je sait d'elle!!!!!. merci pour ta soluce  | |
|
  | |
?
Expert sup

 Nombre de messages : 583 Nombre de messages : 583
Age : 32
Date d'inscription : 27/08/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 12:29 Sam 08 Nov 2008, 12:29 | |
| je pense que la reponse est les nombres qui on E(x)=K
et que K et le carée d un nombre appartient a N
on a E(x²)=E(x)²
<=> E(x)=VE(x²)
donc VE(x²) est un nombre appartient a N donc
E(x²) est le caree dun nombre reel | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 12:32 Sam 08 Nov 2008, 12:32 | |
| tu peux svp expliquer de plus. | |
|
  | |
mhdi
Expert sup
 Nombre de messages : 541 Nombre de messages : 541
Age : 32
Localisation : Tetouan
Date d'inscription : 21/11/2007
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 13:03 Sam 08 Nov 2008, 13:03 | |
| - ? a écrit:
- je pense que la reponse est les nombres qui on E(x)=K
et que K et le carée d un nombre appartient a N
on a E(x²)=E(x)²
<=> E(x)=VE(x²)
donc VE(x²) est un nombre appartient a N donc
E(x²) est le caree dun nombre reel Prends x=2,1 | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 13:06 Sam 08 Nov 2008, 13:06 | |
| - mhdi a écrit:
- La solution de h99 est fausse(enfin, je pense ^^)
Voici la mienne :
Il est évident que Ax£Z : E(x²)=E(x)²
=> Z £ S
Supposons que x £ R\Z
=> x=p+r(p£Z et 0<r<1) =>E(x)²=p²
=> x²=p²+2pr+r² => E(x²)=p²+E(2pr+r²)
Donc, (E(x²)=E(x)² => p²+E(2pr+r²)=p²)
=>E(r²+2pr)=0 =>0=<r²+2pr<1
=>0=<r(r+2p) et r²+2pr<1
Puisque 0<r, -1/2<r/2=<p et r²+2pr<1
p£Z, donc 0=<p et r²+2pr<1
=>0=<p et (p+r)²<p²+1
=>p+r<V(p²+1)
=>p<x<V(p²+1)
=>A={x£R/ p<x<V(p²+1); p£N}UZ £ S
Finalement, on s'assure que Ax£A l'équation est vérifiée. Et on déduit que S=A Bjr Donner une solution qui remplace un iconnu par un autre est tres incorrecte .le debut de ta demarche etait tres bonne mais ta conclusion est a corriger et je croix que tu devais essayer de demontrer que: S=[0;1[UIR | |
|
  | |
mhdi
Expert sup
 Nombre de messages : 541 Nombre de messages : 541
Age : 32
Localisation : Tetouan
Date d'inscription : 21/11/2007
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 13:10 Sam 08 Nov 2008, 13:10 | |
| "je croix que tu devais essayer de demontrer que:
S=[0;1[UIR"
Tu veux surement dire S=[0;1[UZ
Mais si je prend x=2,1, l'équation est bien vérifiée. | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 13:15 Sam 08 Nov 2008, 13:15 | |
| - mhdi a écrit:
- "je croix que tu devais essayer de demontrer que:
S=[0;1[UIR"
Tu veux surement dire S=[0;1[UZ
Mais si je prend x=2,1, l'équation est bien vérifiée. wé ta raison on a :[0;1[UZ C S | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 15:21 Sam 08 Nov 2008, 15:21 | |
| cé un bon exo qui m a fait penser jespere que la slt est achevée! 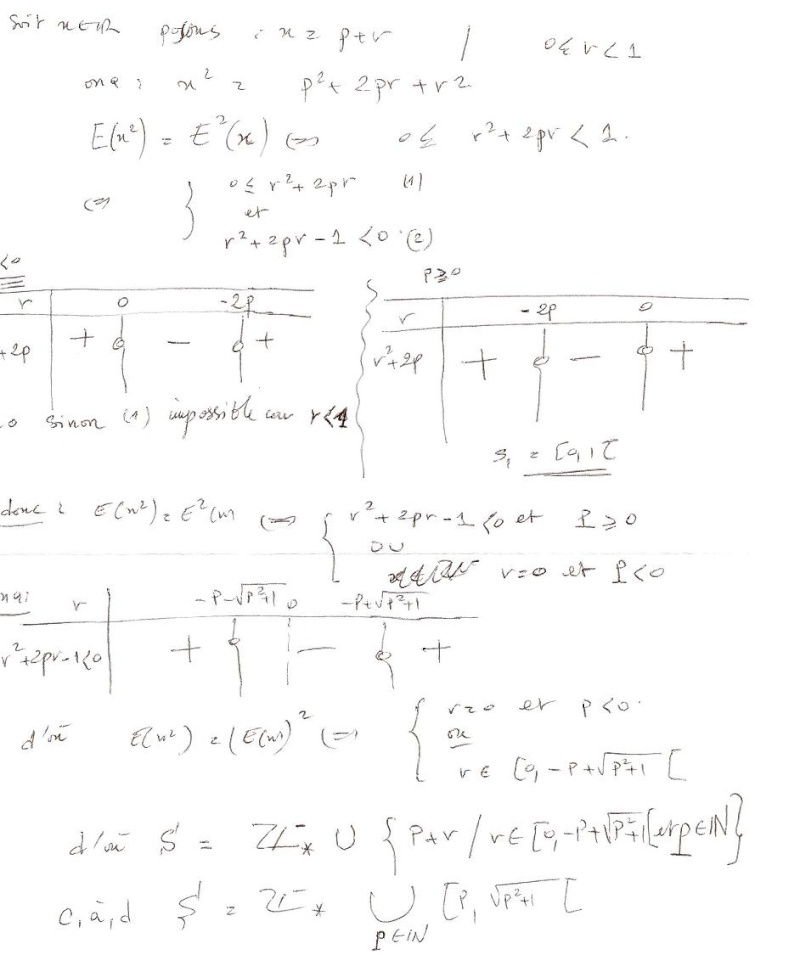
Dernière édition par madani le Dim 09 Nov 2008, 11:14, édité 1 fois | |
|
  | |
miss-Design
Expert grade2

 Nombre de messages : 337 Nombre de messages : 337
Age : 32
Localisation : Agadir
Date d'inscription : 25/10/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 15:44 Sam 08 Nov 2008, 15:44 | |
| bon j'ai trouvé que : 
Dernière édition par miss-Design le Sam 08 Nov 2008, 16:01, édité 1 fois | |
|
  | |
miss-Design
Expert grade2

 Nombre de messages : 337 Nombre de messages : 337
Age : 32
Localisation : Agadir
Date d'inscription : 25/10/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 15:59 Sam 08 Nov 2008, 15:59 | |
| alors la démo:  j'espère que ça soit correct ! 
Dernière édition par miss-Design le Sam 08 Nov 2008, 20:48, édité 1 fois | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 19:59 Sam 08 Nov 2008, 19:59 | |
| - miss-Design a écrit:
- bon j'ai trouvé que :
 wé cé la mm solution que j ai trouvée! | |
|
  | |
miss-Design
Expert grade2

 Nombre de messages : 337 Nombre de messages : 337
Age : 32
Localisation : Agadir
Date d'inscription : 25/10/2008
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  Sam 08 Nov 2008, 20:10 Sam 08 Nov 2008, 20:10 | |
| oui je vois c le même résultat | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: ex logique!!! Sujet: Re: ex logique!!!  | |
| |
|
  | |
| | ex logique!!! |  |
|
