| | les applications (le plat d'aujourd'hui) |  |
|
|
| Auteur | Message |
|---|
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: les applications (le plat d'aujourd'hui) Sujet: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 14:09 Sam 08 Nov 2008, 14:09 | |
| salut tout le monde  | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 14:33 Sam 08 Nov 2008, 14:33 | |
| | |
|
  | |
{}{}=l'infini
Expert sup

 Nombre de messages : 1164 Nombre de messages : 1164
Age : 32
Date d'inscription : 25/09/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 14:47 Sam 08 Nov 2008, 14:47 | |
| les deux premier sont faciles le 3ème :  | |
|
  | |
milor18
Maître
 Nombre de messages : 153 Nombre de messages : 153
Age : 31
Localisation : fes
Date d'inscription : 23/12/2007
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 14:50 Sam 08 Nov 2008, 14:50 | |
| slt, pr le deuxième, la recurrence fera l'affaire le resultat est direct  | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 15:02 Sam 08 Nov 2008, 15:02 | |
| j'ai déjà essayer avec mais sans résultat tu peux montrer comment si c'est possible
pas de réponses pour le premier ? | |
|
  | |
milor18
Maître
 Nombre de messages : 153 Nombre de messages : 153
Age : 31
Localisation : fes
Date d'inscription : 23/12/2007
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 15:15 Sam 08 Nov 2008, 15:15 | |
| raisonnant par récurrence : pr n = 1 f1 = ax+b et a^n*x+b(1-a^n)/(1-a)=ax+b supposons que pr tt n de N la relation donnée est verifiée, et montrons là pr fn+1 fn+1=f(fn)=f(a^n*x+b(1-a^n)/(1-a) ) = a*f(n) + b= a^(n+1)x+ b((a-a^(n+1))/(1-a) + b = a^(n+1)*x+b((a-a^n+1)+1-a /1-a ) = a^(n+1)*x +b(1-a^n+1)/1-a donc fn+1 est aussi vérifié puis conclure  | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 15:41 Sam 08 Nov 2008, 15:41 | |
| exercice 1 pas de réponse .? | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 16:22 Sam 08 Nov 2008, 16:22 | |
| (x+y)(1/x+1/y)=(x+y)²/xy>=4 IAG ==> f bien définie.
Soit t>=4 , (t-2)²-4=t²-4t>=0 ==> il existe h>0 tel que
h²-(t-2)h+1=0 <==> f(h,1)=t . Donc f surjective.
f(x,y)=f(y,x) ( f symétrique) ==> f non injective ( prendre x=1 et y=2) | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 22:28 Sam 08 Nov 2008, 22:28 | |
| - abdelbaki.attioui a écrit:
- (x+y)(1/x+1/y)=(x+y)²/xy>=4 IAG ==> f bien définie.
Soit t>=4 , (t-2)²-4=t²-4t>=0 ==> il existe h>0 tel que
h²-(t-2)h+1=0 <==> f(h,1)=t . Donc f surjective.
f(x,y)=f(y,x) ( f symétrique) ==> f non injective ( prendre x=1 et y=2) peux tu mieux expliquer stp ? et c'est quoi IAG ? | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 22:51 Sam 08 Nov 2008, 22:51 | |
| voila deux autres  | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Sam 08 Nov 2008, 22:51 Sam 08 Nov 2008, 22:51 | |
| svp j'ai besoin de savoir la réponse de ces deux derniers et le premier .
j'ai un DS le lundi
merci d'avance | |
|
  | |
milor18
Maître
 Nombre de messages : 153 Nombre de messages : 153
Age : 31
Localisation : fes
Date d'inscription : 23/12/2007
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Dim 09 Nov 2008, 09:15 Dim 09 Nov 2008, 09:15 | |
| pr la deuxième question : f(n)>=n et non le contraire : puisque f(f(n))>=0 : f(n+1)>=f(n); donc f est croissante raisonnant par recurrence, f(1) >0 donc f(1)>=1 suposons que f(n)>=n et montrons que f(n+1)>=n+1 f(n)>=n => f(fn)>=f(n) ( parce que f est croissante ) donc f(n+1)-f(n)>=f(n) f(n+1)>=2f(n)>=2n>=n+1 ( parce n>=1 ) puis conclure, bonne chance pr le DS  | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Dim 09 Nov 2008, 12:12 Dim 09 Nov 2008, 12:12 | |
| f(n,p)=f(n',p') <==> 1+...+(n+p)+p=1+...+(n'+p')+p'
si n+p>n'+p' alors (n'+p'+1)+...+(n+p)+p=p' absurde
==> n+p=n'+p' ==> p=p' ==> n=n' cqfd | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Dim 09 Nov 2008, 12:35 Dim 09 Nov 2008, 12:35 | |
| merci M. milor18 merci M.abdelbaki.attioui
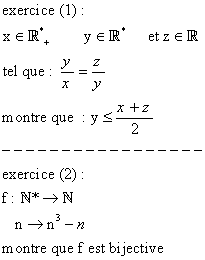
| |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Dim 09 Nov 2008, 12:36 Dim 09 Nov 2008, 12:36 | |
| voila d'autres que j'arrive pas a faire | |
|
  | |
milor18
Maître
 Nombre de messages : 153 Nombre de messages : 153
Age : 31
Localisation : fes
Date d'inscription : 23/12/2007
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Dim 09 Nov 2008, 15:06 Dim 09 Nov 2008, 15:06 | |
| pr le deuxième exo, f ne peut etre bijective car f n'est po surjective, la preuve : n^3-n=n(n-1)(n+1) est un nombre pair, donc f(n)=m n'a pas de solutions si m est impair, donc f n'est pas surjective et par conséquent, n'est pas bijective ( par contre, f est une injection, si tu veux la demonstration, t'as qu'à demander )  | |
|
  | |
milor18
Maître
 Nombre de messages : 153 Nombre de messages : 153
Age : 31
Localisation : fes
Date d'inscription : 23/12/2007
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Dim 09 Nov 2008, 15:11 Dim 09 Nov 2008, 15:11 | |
| pr le premier exercice il suffit de remarquer que y^2=xz, donc on a deux cas : y>0
y=rac(xz) et nous savons que ( rac(x)-rac(z))^2>=0 donc x+z>=2rac(xz) => (x+z)/2>=rac(xz) = y
y est negatif, dans ce cas là y/x est negatif, donc z/y l'est aussi, donc z est positif, d'où (x+y)/2 > 0 > y
et voilà ! | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Dim 09 Nov 2008, 15:17 Dim 09 Nov 2008, 15:17 | |
| | |
|
  | |
milor18
Maître
 Nombre de messages : 153 Nombre de messages : 153
Age : 31
Localisation : fes
Date d'inscription : 23/12/2007
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Dim 09 Nov 2008, 15:25 Dim 09 Nov 2008, 15:25 | |
| c'est un plaisir
PS: ces exos sont super interessants, d'où ce que tu les deniches ? xD !! | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Dim 09 Nov 2008, 19:45 Dim 09 Nov 2008, 19:45 | |
|  de notre manuel il est plein d'exos de ce genre et aussi notre prof nous fais noyez d'exos rares et intéressants | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Lun 17 Nov 2008, 15:26 Lun 17 Nov 2008, 15:26 | |
| - milor18 a écrit:
- pr le premier exercice il suffit de remarquer que y^2=xz, donc on a deux cas : y>0
y=rac(xz) et nous savons que ( rac(x)-rac(z))^2>=0 donc x+z>=2rac(xz) => (x+z)/2>=rac(xz) = y
y est negatif, dans ce cas là y/x est negatif, donc z/y l'est aussi, donc z est positif, d'où (x+y)/2 > 0 > y
et voilà ! svp comment t'as su que y^2=xz ? | |
|
  | |
milor18
Maître
 Nombre de messages : 153 Nombre de messages : 153
Age : 31
Localisation : fes
Date d'inscription : 23/12/2007
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Lun 17 Nov 2008, 15:29 Lun 17 Nov 2008, 15:29 | |
| puisque y/x=z/y ( le produit des extremes egale le produit des moyens ) | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 | |
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Lun 17 Nov 2008, 17:36 Lun 17 Nov 2008, 17:36 | |
| - abdelbaki.attioui a écrit:
- (x+y)(1/x+1/y)=(x+y)²/xy>=4 IAG ==> f bien définie.
Soit t>=4 , (t-2)²-4=t²-4t>=0 ==> il existe h>0 tel que
h²-(t-2)h+1=0 <==> f(h,1)=t .Donc f surjective.
f(x,y)=f(y,x) ( f symétrique) ==> f non injective ( prendre x=1 et y=2) SVP les amis j'ai pas compris cette ligne .. Veuillez m'aider ... et merci | |
|
  | |
dangerous mind
Expert sup

 Nombre de messages : 576 Nombre de messages : 576
Age : 32
Localisation : fes , maroc
Date d'inscription : 08/07/2008
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  Lun 17 Nov 2008, 17:56 Lun 17 Nov 2008, 17:56 | |
| bon vraiment moi aussi je l'ai pas compris mais voila ma méthode pour l'injectivité c'est clair mais pour surjectivité tu vas poser que x/y = t et y/x = 1/t après tu vas trouver la solution et conclure | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: les applications (le plat d'aujourd'hui) Sujet: Re: les applications (le plat d'aujourd'hui)  | |
| |
|
  | |
| | les applications (le plat d'aujourd'hui) |  |
|
