| | Problème de la semaine N°189 (08/06/2009-14/06/2009) |  |
|
+5charaf exp badr_210 houssa joystar1 samir 9 participants |
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Lun 08 Juin 2009, 10:53 Lun 08 Juin 2009, 10:53 | |
| | |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Lun 08 Juin 2009, 10:56 Lun 08 Juin 2009, 10:56 | |
| salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci | |
|
  | |
joystar1
Maître
 Nombre de messages : 148 Nombre de messages : 148
Age : 35
Date d'inscription : 17/03/2007
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Lun 08 Juin 2009, 15:20 Lun 08 Juin 2009, 15:20 | |
| | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Mar 09 Juin 2009, 07:08 Mar 09 Juin 2009, 07:08 | |
| soltion postée
.......................... | |
|
  | |
badr_210
Expert grade2

 Nombre de messages : 327 Nombre de messages : 327
Age : 33
Localisation : Sidi Slimane
Date d'inscription : 07/07/2007
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Mar 09 Juin 2009, 11:20 Mar 09 Juin 2009, 11:20 | |
| Solution postée
on note ( E) l'équation ( sin (x)+sin(2x)+sin(3x))²+(cos(x)+cos(2x)+cos(3x))²=1
(E) <==> 3+2(sin(x)sin(2x)+cos(x)cos(2x)+sin(2x)sin(3x)+cos(2x)cos(3x)+sin(x)sin(3x)+cos(x)cos(3x)=1
<==> 3+2(2cos(x)+cos(2x))=1
==> 2cos(x)+cos(2x)=-1
==> 2cos(x)+2cos²(x)=0
==> cos(x) =0 ou cos(x)=-1
==> x=kpi/2 ou x = pi + 2kpi / k €Z
les solutions vérifient l'équation
d'où S= { kpi/2 , pi + 2kpi / k € Z }
| |
|
  | |
charaf exp
Féru
 Nombre de messages : 33 Nombre de messages : 33
Age : 33
Date d'inscription : 01/09/2008
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Mar 09 Juin 2009, 13:45 Mar 09 Juin 2009, 13:45 | |
| | |
|
  | |
khamaths
Maître
Nombre de messages : 98
Date d'inscription : 17/03/2006
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Mer 10 Juin 2009, 10:29 Mer 10 Juin 2009, 10:29 | |
| Bonjour
Solution postée
* sinx +sin2x+sin3x= sin2x+2sin2x.cosx = sin2x .(1+2cosx)
* cosx +cos2x+ cos3x = cos 2x + 2cos 2x.cosx = cos2x.(1+ 2cosx)
L'équation en question <====> (1+2cosx)² =1
<====>1+2cosx =1 ou -1
<====> cosx= 0 ou cos x= -1
<====> x= (pi /2)+kpi ou x= pi +2kpi / k £ Z | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Mer 10 Juin 2009, 12:36 Mer 10 Juin 2009, 12:36 | |
| Salut. Première participation  Solution postée. Solution postée. | |
|
  | |
Boomer
Maître

 Nombre de messages : 140 Nombre de messages : 140
Age : 32
Localisation : lC
Date d'inscription : 18/07/2008
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Ven 12 Juin 2009, 00:30 Ven 12 Juin 2009, 00:30 | |
| solution postée 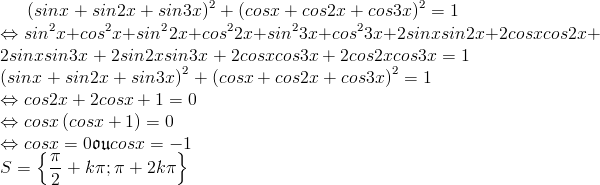 | |
|
  | |
MouaDoS
Expert sup

 Nombre de messages : 601 Nombre de messages : 601
Age : 32
Localisation : Près de + l'infini
Date d'inscription : 08/12/2008
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  Sam 13 Juin 2009, 14:04 Sam 13 Juin 2009, 14:04 | |
| Solution Postee
(cos(x)+cos(2x)+cos(3x))² + (sin(x)+sin(2x)+sin(3x))²=1
<=> 3+2(cos(x).cos(2x) + sin(x).sin(2x) + cos(x).cos(3x) + sin(x).sin(3x) + cos(2x).cos(3x) + sin(2x).sin(3x)) = 1
<=> 2cos(x) + cos(2x)=-1
<=> cos(x)[cos(x)+1]=0
S={pi/2+k.pi , pi+2k.pi / k€Z} | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009) Sujet: Re: Problème de la semaine N°189 (08/06/2009-14/06/2009)  | |
| |
|
  | |
| | Problème de la semaine N°189 (08/06/2009-14/06/2009) |  |
|
