| | INégo |  |
|
+4Perelman . EINSTEINIUM samix 8 participants |
| Auteur | Message |
|---|
samix
Expert grade2
 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
| | Sujet: INégo Mar 27 Oct 2009, 22:29 | |
| Salut, x,y,z>0 M.Q  | |
|
| | |
EINSTEINIUM
Maître
Nombre de messages : 245
Age : 31
Localisation : Oujda
Date d'inscription : 29/01/2009
| | Sujet: Re: INégo Mar 27 Oct 2009, 23:27 | |
| On a :  Donc on a  et on sait que  et que  (Nesbit inequality) Donc : 
Dernière édition par EINSTEINIUM le Mar 27 Oct 2009, 23:33, édité 1 fois | |
|
| | |
.
Maître
Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
| | Sujet: Re: INégo Mer 18 Nov 2009, 17:51 | |
| il existe une autre solution sans théorème  | |
|
| | |
Perelman
Expert sup
Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
| | Sujet: Re: INégo Mar 15 Déc 2009, 00:08 | |
| slt!! ma solution: l'inego est homogène on mets x+y+z=1 donc: par cauchy:  donc suffit de prouver que:  ce qui est juste!. | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: INégo Mar 15 Déc 2009, 16:34 | |
| Le terme à gauche est symétrique, alors on peut supposer que 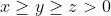 . Ainsi, 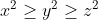 et (z+2y)}\geq&space;\frac{1}{(2x+z)(2z+x)}&space;\geq&space;\frac{1}{(2x+y)(2y+x)}) . \sum&space;_{cyc}\frac{1}{(2z+y)(z+2y)}) , d'après Chebyschev. \frac{1}{4(x^{2}+y^{2}+z^{2})+5(xy+yz+xz)}) , d'après Cauchy-Schwartz. Mais il est bien connu que  . D'où \frac{1}{9(x^{2}+y^{2}+z^{2})}&space;=&space;\frac{1}{3}) , CQFD. | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: INégo Mer 16 Déc 2009, 13:32 | |
| C'est aussi possible par AM.GM je pense !! | |
|
| | |
{}{}=l'infini
Expert sup
Nombre de messages : 1164
Age : 32
Date d'inscription : 25/09/2008
| | Sujet: Re: INégo Jeu 17 Déc 2009, 06:05 | |
| salut tous le monde !
salut Hamza !
peux - tu expliquer un peu ta méthode ? | |
|
| | |
Perelman
Expert sup
Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
| | Sujet: Re: INégo Jeu 17 Déc 2009, 13:22 | |
| - {}{}=l'infini a écrit:
- salut tous le monde !
salut Hamza !
peux - tu expliquer un peu ta méthode ? homogénéité<==>a+b+c=1+cauchy==>résultat; c clair je pense!. | |
|
| | |
Thalès
Expert grade1
Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
| | Sujet: Re: INégo Jeu 17 Déc 2009, 21:01 | |
| Je pense que ce qui te pose problème c'est le fait d'avoir considéré : x+y+z=1
Remarque que : (x;y;z) vérifie l'inégalité <=> (kx;ky;kz) vérifie l'inégalité pour tout k€R*
Donc quelque soit x,y et z, il existe un a tel que x+y+z=a <=> x/a+y/a+z/a=1 donc on peux toujours se rammener au fait que la somme donne 1 en posant X=x/a; Y=y/a et Z=z/a => X+Y+Z=1
Donc si on travaille avec x+y+z=1 ça ne change rien, l'inégalité est homogène | |
|
| | |
Perelman
Expert sup
Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
| | Sujet: Re: INégo Jeu 17 Déc 2009, 21:27 | |
| oui merci d'avoir écrit ces détails  (je suis paresseux^^) | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: INégo | |
| |
|
| | |
| | INégo | |
|
