Résolution d'une équation

Bonjour tout le monde
SVP aidez moi à résoudre cette équation dans Z
racine(1+racine(x+2)=4038+racine(x+2)+x
merci

Je donne ma solution:
Posons: .
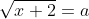
On a .
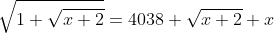
Donc .
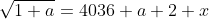
Donc .
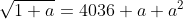
Donc .
Donc .
Donc .
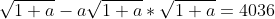
Donc .
Puisqu'on veut résoudre l'équation en Z, on cherche les diviseurs de 4036, qui sont 4036-1-2-2018-4-1009.
Et on a 4036=4036*1=1*4036.
Et 4036=2018*2=2*2018.
Et 4036=1009*4=4*1009.
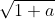
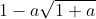
D'autre part on a un nombre positif donc l'est aussi.
Et on a .
Et on a V(x+2) est positif.
Donc V(x+2)>=0.
Donc a>=0.
Donc a+1>=1.
Et V(a+1)>=1.
Donc (a+1)V(a+1)>=1.
Finalement 0>=1-(a+1)V(a+1).
Soit 0>=1-aV(1+a)-V(1+a).
Donc V(1+a)>=1-aV(1+a).
Le premier cas V(1+a)=4036 et 1-aV(1+a)=1.
On a 1-aV(1+a)=1.
Donc -aV(1+a)=0.
Donc aV(1+a)=0.
Donc a=0 car a est supérieur à 1.
Cette valeur ne réalise pas l'autre équation.
Le deuxième cas V(1+a)=2018 et 1-aV(1+a)=2.
On a 1-aV(1+a)=2.
Donc -aV(1+a)=1.
Donc aV(1+a)=-1.
Ce qui est impossible car a et V(1+a) sont positifs.
Le deuxième cas V(1+a)=1009 et 1-aV(1+a)=4.
On a 1-aV(1+a)=4.
Donc -aV(1+a)=3.
Donc aV(1+a)=-3.
Ce qui est impossible car a et V(1+a) sont positifs.
On conclut que l'équation proposée n'a pas de solution dans Z.
J'attend vos reclamation à propos de cette démonstration.