| | inegalite triangle |  |
|
|
| Auteur | Message |
|---|
Pedro thunder
Habitué

 Nombre de messages : 18 Nombre de messages : 18
Age : 31
Date d'inscription : 01/12/2009
 |  Sujet: inegalite triangle Sujet: inegalite triangle  Ven 08 Jan 2010, 20:43 Ven 08 Jan 2010, 20:43 | |
| ABC est un triangle
a=BC b=AC c=AB
prouver que
(a²+b²-c²)(a²+c²-b²)(b²+c²-a²)<=a²b²c² | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Ven 08 Jan 2010, 21:06 Ven 08 Jan 2010, 21:06 | |
| On a :
a+b>c
a²>b²+c²-2bc car a>|b-c|
d'où
b²+c²-a²<2bc de même
a²+b²-c²<2ab
a²+c²-b²<2ac
Si l'un des facteur à gauche est négative l'inégo est vérifié car les 2 autres seront positive ...
Donc on peut supposer que tous les facteurs sont positive alors on a :
(a²+b²-c²)(a²+c²-b²)(b²+c²-a²)<2ab2bc2ac=8a²b²c² | |
|
  | |
Pedro thunder
Habitué

 Nombre de messages : 18 Nombre de messages : 18
Age : 31
Date d'inscription : 01/12/2009
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Sam 09 Jan 2010, 12:36 Sam 09 Jan 2010, 12:36 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Sam 09 Jan 2010, 13:10 Sam 09 Jan 2010, 13:10 | |
| a², b² et c² étant les longueurs de côtés d'un triangle, a,b et c le sont aussi. Il revient donc à prouver que (a+c-b)(b+c-a)\leq%20abc) qui n'est autre que l'inégalité de Padoa. L'inégalité présentée ici est toutefois bien plus faible que celle de Padoa. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Ven 22 Jan 2010, 18:47 Ven 22 Jan 2010, 18:47 | |
| Si l'un des facteur à gauche est négative donc l'inégo est vérifié on peut supposer que tous les facteurs sont positifs ..
On pose :
x=a²+b²-c² y=a²+c²-b² z=b²+c²-a²
On a donc :
a²=x+y/2 b²=x+z/2 c²=y+z/2
L'inégo équivaut à :
8xyz≤(x+y)(x+z)(y+z)
Ce qui est vrai .. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Ven 22 Jan 2010, 21:16 Ven 22 Jan 2010, 21:16 | |
| - Sylphaen a écrit:
L'inégo équivaut à :
8xyz≤(x+y)(x+z)(y+z)
Ce qui est vrai .. Elle est vraie ssi x,y et z sont supposés positifs, ou, d'une manière équivalente, 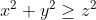 , et cycliquement. Mais cela ne peut être déduit de l'énoncé. Aussi, ma solution précédente est tout à fait fausse, car repose sur des interprétations sujettes à défaut. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Ven 22 Jan 2010, 21:22 Ven 22 Jan 2010, 21:22 | |
| Bin si on a : z²>=x²+y² donc z²+x²>y² et z²+y²>x² Donc LHS est négatif et l'inégo est vérifié .. Ce qui nous mène vers le cas où LHS est positifs et on fait le changement de variable  | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Ven 22 Jan 2010, 22:03 Ven 22 Jan 2010, 22:03 | |
| salam
El Kashi ====> a²=b²+c²-2bc.cosA =====> b²+c²-a² = 2bc.cosA
etc .........
le produit = 8a²b²c².cosA.cosB.cosC à majorer........
en tenant compte de A+B+C= 180°
. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Ven 22 Jan 2010, 22:27 Ven 22 Jan 2010, 22:27 | |
| - Dijkschneier a écrit:
- Sylphaen a écrit:
L'inégo équivaut à :
8xyz≤(x+y)(x+z)(y+z)
Ce qui est vrai .. Elle est vraie ssi x,y et z sont supposés positifs, ou, d'une manière équivalente, 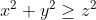 , et cycliquement. , et cycliquement.
Mais cela ne peut être déduit de l'énoncé.
Aussi, ma solution précédente est tout à fait fausse, car repose sur des interprétations sujettes à défaut. je crois que la meilleure solution est celle du changement des variables qu'a fait Sylphaen... à Dijkschneier...le cas où (a²+b²-c²)(c²+a²-b²)(b²+c²-a²)=<0 est trivial alors il nous reste de voir les cas où (a²+b²-c²)(c²+a²-b²)(b²+c²-a²)>=0 et sont : tous les thermes sont positifs.... ou l'un est positif et les deux autres sont négatifs... supposons donc que ces deux termes négatifs sont a²+b²-c² et c²+a²-b² alors a²+b²<c² et c²+a²<b² ==>2a²<0 ce qui est absurde alors au moins l'un des deux est positif ce qui implique tous les termes sont positifs.... ou deux termes positif et l'un négatif==>(a²+b²-c²)(c²+a²-b²)(b²+c²-a²)=<0 qui est un cas trivial ainsi on peut supposer que a²+b²>c² et b²+c²>a² et a²+c²>b²  sauf erreur.... | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Sam 23 Jan 2010, 12:40 Sam 23 Jan 2010, 12:40 | |
| - majdouline a écrit:
à Dijkschneier...le cas où (a²+b²-c²)(c²+a²-b²)(b²+c²-a²)=<0 est trivial
alors il nous reste de voir les cas où (a²+b²-c²)(c²+a²-b²)(b²+c²-a²)>=0
et sont : tous les thermes sont positifs.... ou l'un est positif et les deux autres sont négatifs...
supposons donc que ces deux termes négatifs sont a²+b²-c² et c²+a²-b² alors a²+b²<c² et c²+a²<b² ==>2a²<0 ce qui est absurde alors au moins l'un des deux est positif ce qui implique tous les termes sont positifs.... ou deux termes positif et l'un négatif==>(a²+b²-c²)(c²+a²-b²)(b²+c²-a²)=<0 qui est un cas trivial
ainsi on peut supposer que a²+b²>c² et b²+c²>a² et a²+c²>b² 
sauf erreur.... J'y consens. La démonstration de Sylphaen, bien que peu loquace, est finalement correcte. | |
|
  | |
codex00
Expert sup

 Nombre de messages : 2122 Nombre de messages : 2122
Age : 34
Localisation : No where !!!
Date d'inscription : 30/12/2006
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  Sam 23 Jan 2010, 18:01 Sam 23 Jan 2010, 18:01 | |
| - houssa a écrit:
- salam
El Kashi ====> a²=b²+c²-2bc.cosA =====> b²+c²-a² = 2bc.cosA
etc .........
le produit = 8a²b²c².cosA.cosB.cosC à majorer........
en tenant compte de A+B+C= 180°
. pour majorer CosA.cosB.cosC il suffit d'appliquer jensen sur f(x)=-ln(cosx) on trouve cosA.cosB.cosC=<1/8 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: inegalite triangle Sujet: Re: inegalite triangle  | |
| |
|
  | |
| | inegalite triangle |  |
|
