Soit n un entier arbitraire, et soit A le produit de quatre nombres entiers consécutifs augmenté de 1.
A peut être noté
(n+2)(n+3)+1)
Donc
(n+2)(n+3)+1)
.
Donc
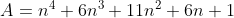
.
Donc
^2)
.
On a
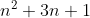
est entier, par construction de n, et de fait,
^2)
est un carré parfait qu'on note s.
Donc
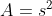
.
Supposons que le produit de quatre entiers naturels consécutifs est un carréparfait.
Donc, il existe un entier t vérifiant
(n+2)(n+3))
.
On a
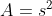
.
Donc
(n+2)(n+3)+1=s^2)
.
Donc
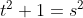
.
Donc
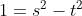
.
Donc
(s+t))
.
Donc
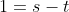
et
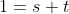
.
Par addition, on trouve
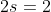
.
Donc
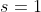
.
Et par conséquant
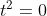
.==>(1)
Et puisque ni n, ni n+1, ni n+2, ni n+3, est nul.
Il vient que
(n+2)(n+3))
n'est pas nul.
Donc
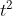
n'est pas nul.==>(2)
Il y a une contradiction entre 1 et 2, ce qui fait que la supposition est fausse.
Donc le produit de quatre entiers naturels consécutifs et non nuls ne
peut pas être un carré parfait.
CQFD.
