Deux exercices du livres du maths:

Le premier:
Montrez que pour tout entiers a,b,c, et d supérieurs ou égal à 2
Et a#b#c#d.
V[(1-1/a^2)(1-1/b^2)(1-1/c^2)(1-1/d^2)]>=(V2)/2.
Le deuxième:
Montrez que:
(V5)/6+(V20)/9+(V42)/13+....+(V2n(n+1))/4n+1=<n/2.
Bonne chance.

1/
Par symétrie des rôles, on peut supposer que : .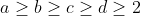
a,b,c et d étant des entiers distincts, on a : .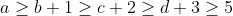
D'où :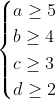

Ainsi,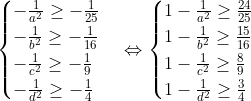

Par multiplication :

Pour le deuxième, la suite ne semble pas être très bien construite.

Pour le premier, j'ai fait la même chose.
Mais pour le deuxième, il est faux je pense qu'il fallait dire:
Montrez que:
(V5)/6+(V20)/9+(V42)/13+....+(V2n(2n+1))/4n+1=<n/2.
Bonne chance.

nmo a écrit:

Pour le premier, j'ai fait la même chose.
Mais pour le deuxième, il est faux je pense qu'il fallai dire:
Montrez que:
(V5)/6+(V20)/9+(V42)/13+....+(V2n(2n+1))/4n+1=<n/2.
Bonne chance.

Je vous donne la réponse le jeudi prochain si je ne trouve pas de réponse.

Le deuxième serait plutôt :.
Solution
Il est connu d'après l'IAG que : , d'où
Le résultat s'ensuit en sommant.