Deux exercices

Sujet: Deux exercices Ven 22 Jan 2010, 17:01

Le premier:
On écrit le nombre suivat composé d'une série des chiffres de 1,2,3,...
Et ainsi de suite jusqu'a 2009.
A=0.1234567891011121314151617..................20082009.
Combien y-a-t-il de chiffres après la virgule du nombre A.
Le deuxième:
Soit ABCD un polygone convexe et E le milieu de BC et F celui de AD.
On pose AB=c et AC=b et BC=a.
1-Montrez que la somme des surfaces des triangles FBC et EDA égale la surface de ABCD.
2-Montrez que: a/(b+c) +b/(c+a) + c/(a+b) <2.
Bonne chance.

Sujet: Re: Deux exercices Ven 22 Jan 2010, 18:35

Pour le 1 :
De 1->9 on a 9 chiffre
De 10->99 On a 2 (99-10+1)=180
De 100-999 on a 3(999-100+1)=2700
De 1000->2009 on a 4(2009-1000+1)=4040

Donc de 1->2009 on a : 9+180+2700+4040=6929 chiffres

Sauf erreur Smile

Sujet: Re: Deux exercices Mar 16 Mar 2010, 19:29

Pour le le deuxième:
Premièrement:
Avant de répondre:
Soit ABC un triangle et M le milieu de [BC] et h la hauteur passant par A.
On a BM=MC.
Donc BM*h=MC*h.
Donc (BM*h)/2=(MC*h)/2.
Finalement S(ABM)=S(AMC).
Maintenant au travail:
On a E est le milieu de (BC).
Et on a F est le milieu de (AD).
En utilisant la méthode que je viens d'annocer.
On trouve:
S(ABF)=S(FBD).
S(EAF)=S(EFD).
S(CFD)=S(CFA).
S(ABE)=S(AEC).
S(FBE)=S(FEC).
S(DEC)=S(DEB).
On a S(ABCD)=S(ABF)+S(FBE)+S(FED)+S(DEC).
Donc S(ABCD)=S(FBD)+S(FEC)+S(AEF)+S(DEB).
Donc S(ABCD)=S(FDB)+S(DEB)+S(FEC)+S(AEF).
Donc S(ABCD)=S(BFDE)+S(FEC)+S(AEF).
Donc S(ABCD)=S(FBE)+S(FED)+S(FEC)+S(AEF).
Donc S(ABCD)=S(FBE)+S(FEC)+S(FED)+S(AEF).
Donc S(ABCD)=S(FBC)+S(EDA).
CQFD.
Deuxièmement:
On souhaite démontrer que: a/(b+c) +b/(c+a) + c/(a+b) <2.
C'est à dire a(a+c)(a+b)+b(b+a)(b+c)+c(c+a)(c+b)<2(a+b)(b+c)(c+a).
On a a(a+c)(a+b)+b(b+a)(b+c)+c(c+a)(c+b)=a(a^2+ab+ac+bc)+b(b^2+bc+ab+ac)+c(c^2+cb+ca+ab).
Donc a(a+c)(a+b)+b(b+a)(b+c)+c(c+a)(c+b)=a^3+a^2*b+a^2*c+abc+b^3+b^2*c+b^2*a+abc+c^3+c^2*b+c^2*a+abc.
Donc a(a+c)(a+b)+b(b+a)(b+c)+c(c+a)(c+b)=a^3+b^3+c^3+a^2*(b+c)+b^2*(a+c)+c^2*(a+b)+3abc.
Et on a 2(a+b)(b+c)(c+a)=2(a+b)(bc+ba+c^2+ca).
Donc 2(a+b)(b+c)(c+a)=2(abc+a^2b+c^2a+a^2c+b^2c+b^2a+c^2b+abc).
Donc 2(a+b)(b+c)(c+a)=2[a^2*(b+c)+b^2*(a+c)+c^2*(a+b)+2abc].
Donc 2(a+b)(b+c)(c+a)=2a^2*(b+c)+2b^2*(a+c)+2c^2*(a+b)+4abc.
Et on fait la soustraction: 2(a+b)(b+c)(c+a)-a(a+c)(a+b)+b(b+a)(b+c)+c(c+a)(c+b)=2a^2*(b+c)+2b^2*(a+c)+2c^2*(a+b)+4abc-[a^3+b^3+c^3+a^2*(b+c)+b^2*(a+c)+c^2*(a+b)+3abc].
Donc 2(a+b)(b+c)(c+a)-a(a+c)(a+b)+b(b+a)(b+c)+c(c+a)(c+b)=2a^2*(b+c)+2b^2*(a+c)+2c^2*(a+b)+4abc-a^3-b^3-c^3-a^2*(b+c)-b^2*(a+c)-c^2*(a+b)-3abc.
Donc 2(a+b)(b+c)(c+a)-a(a+c)(a+b)+b(b+a)(b+c)+c(c+a)(c+b)=a^2*(b+c)+b^2*(a+c)+c^2*(a+b)+abc-a^3-b^3-c^3.
Et on a a; b; et c les longueurs d'un triangle.
Donc b+c>a.
Donc a^2*(b+c)>a*a^2.
Donc a^2*(b+c)>a^3.
De même: b^2*(a+c)>b^3.
Et c^2*(a+b)>c^3.
Donc, en sommant a^2*(b+c)+b^2*(a+c)+c^2*(a+b)>a^3+b^3+c^3.
Donc a^2*(b+c)+b^2*(a+c)+c^2*(a+b)-a^3-b^3-c^3>0.==>(1)
D'autre part, on a abc>0.==>(2)
Et en sommant 1 et 2 a^2*(b+c)+b^2*(a+c)+c^2*(a+b)+abc-a^3-b^3-c^3.
Donc a(a+c)(a+b)+b(b+a)(b+c)+c(c+a)(c+b)<2(a+b)(b+c)(c+a).
Soit en résumé a/(b+c) +b/(c+a) + c/(a+b) <2.
CQFD.
Sauf faute de frappe.

Sujet: Re: Deux exercices Mar 16 Mar 2010, 19:57

Solution du Problem N°2:
Puisque a,b,c sont les coté d'un triangle, on a donc:
2(a+b)=(a+b)+(a+b)>=a+b+c, alors a+b>= 1/2 (a+b+c)
de même on trouve que: b+c>=1/2(a+b+c) et c+a>=1/2 (a+b+c). Alors:
a/(b+c) + b/(a+c) + c/(a+b) >=1/2 [a/(a+b+c)+b/(a+b+c)+c/(a+b+c)]=1/2
avec égalité si et seulement si a=b+c et c=a+b et b=a+c
=>a=b=c=0 ce qui est absurde car a,b,c sont les longueures des côté d'un triangle. d'où on déduit que:
a/(b+c) + b/(a+c) + c/(a+b) > 1/2.

Sujet: Re: Deux exercices Mar 16 Mar 2010, 20:00

MohE a écrit:: Solution du Problem N°2:
Puisque a,b,c sont les coté d'un triangle, on a donc:
2(a+b)=(a+b)+(a+b)>=a+b+c, alors a+b>= 1/2 (a+b+c)
de même on trouve que: b+c>=1/2(a+b+c) et c+a>=1/2 (a+b+c). Alors:
a/(b+c) + b/(a+c) + c/(a+b) >=1/2 [a/(a+b+c)+b/(a+b+c)+c/(a+b+c)]=1/2
avec égalité si et seulement si a=b+c et c=a+b et b=a+c
=>a=b=c=0 ce qui est absurde car a,b,c sont les longueures des côté d'un triangle. d'où on déduit que:
a/(b+c) + b/(a+c) + c/(a+b) > 1/2.

Ce n'est pas ce qu'il fallait démontré mais c'est juste.
J'ai dit: Montrez que: a/(b+c) +b/(c+a) + c/(a+b) <2.
Regarde l'énoncé.

Sujet: Re: Deux exercices Mer 17 Mar 2010, 13:25

Pour le premier :

[1,9] : Il ya 9 Chiffres.
[10,99] : Il ya (99-10)+1=90 Chiffres.
[100,999] : Il ya (999-100)+1=900 Chiffres.
[1000,2009] : Il ya (2009-1000)+1= 1010 Chiffres.

Donc : Il ya 2009 Chiffres aprés la virgule.

Sujet: Re: Deux exercices Mer 17 Mar 2010, 13:33

Pour le deuxiéme :

1/ Soit R le point d'interction de (FC) et (ED) , soit R le point d'interction de (AE) et (FB)

Il suffit donc de montrer que :
S (drc) + S (azb) = S (frez)

Sujet: Re: Deux exercices Mer 17 Mar 2010, 18:10

nmo a écrit:: 2-Montrez que: a/(b+c) +b/(c+a) + c/(a+b) <2.

Sachant que ce sont les côtés d'un triangle, ça devient trivial. C'est le premier exercice proposé chez Animath, pour vous dire combien c'est facile.
$Deux exercices Gif$
(Puisqu'on sait que : 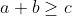$Deux exercices Gif$ ... etc)
D'autres façons de faire existent, mais je vous propose une autre inégalité facile à faire aussi :
$Deux exercices Gif$ n et un entier, et a,b > 0
Trois méthodes au minimum, pour corser les choses (j'en ai trouvé "au moins" 4 ou 5)

Sujet: Re: Deux exercices Jeu 18 Mar 2010, 18:43

oussama1305 a écrit:: mais je vous propose une autre inégalité facile à faire aussi :
$Deux exercices Gif$ n et un entier, et a,b > 0
Trois méthodes au minimum, pour corser les choses (j'en ai trouvé "au moins" 4 ou 5)

Voici la première methode:
On a (a-b)²>=0.
Donc a²-2ab+b²>=0.
Donc a²+b²>2ab.
Donc a²+b²+2ab>=2ab+2ab.
Donc (a+b)²>=4ab.
Donc a+b>=2Vab.==>(*) Si a et b sont positifs.
En utilisant *, on prend a=(1+a/b)^n et b=(1+b/a)^n.
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .==>(a)
D'autre part, en utilisant *, on prend a=1 et b=a/b.
Donc 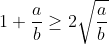$Deux exercices Gif$ .
Donc $Deux exercices Gif$ .==>(1)
De même $Deux exercices Gif$ .==>(2)
En multipliant 1 et 2, on obtient $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .==>(b)
Et de a et b, on conclut que $Deux exercices Gif$ .
CQFD.

Sujet: Re: Deux exercices Jeu 18 Mar 2010, 19:54

Bjr Oussama ; Voici une deuxiéme methode qui coute moin chér ))

Premiérement on a : (a+b)^n>a^n+b^n (1) puisque (a,b >0) alors : 4^n>2^n+1
On a : ((a/b+1))^n>=2^n et ((b/a+1))^n>=2^n
Donc : ((a/b+1))^n((b/a+1))^n>=4^n
Donc : 2V((a/b+1)^n((b/a+1)^n>=4^n>=2^n+1 (car : 2^n*2^n>=2^n+1)
de méme on a : ((1+a/b))^n + ((1+b/a))^n>= 2V((a/b+1)^n((b/a+1)^n ( d'aprés a+b>=2Vab (a,b>0) )
Dont le résultat ^^

Sujet: Re: Deux exercices Ven 19 Mar 2010, 11:41

M.Marjani a écrit:: Bjr Oussama ; Voici une deuxiéme methode qui coute moin chér ))

Premiérement on a : (a+b)^n>a^n+b^n (1) puisque (a,b >0) alors : 4^n>2^n+1
(1+b/a)^n>=2^n et (1+a/b)^n>=2^n
Veut dire que : ((a/b+1))^n((b/a+1))^n>=4^n
Donc : 2V((a/b+1)^n((b/a+1)^n>=4^n>=2^n+1 (d'aprés (1))
de méme on a : ((1+a/b))^n + ((1+b/a))^n>= 2V((a/b+1)^n((b/a+1)^n ( d'aprés a+b>=2Vab (a,b>0) )
Dont le résultat ^^

Prends b=1 et a=1000.
Ce qui est en rouge est faux.
L'autre inégalité qui la suit est fausse.

Sujet: Re: Deux exercices Ven 19 Mar 2010, 13:06

nmo a écrit:

oussama1305 a écrit:: mais je vous propose une autre inégalité facile à faire aussi :
$Deux exercices Gif$ n et un entier, et a,b > 0
Trois méthodes au minimum, pour corser les choses (j'en ai trouvé "au moins" 4 ou 5)

Voici la première methode:
On a (a-b)^2>=0.
Donc a^2-2ab+b^2>=0.
Donc a^2+b^2>2ab.
Donc a^2+b^2+2ab>=2ab+2ab.
Donc (a+b)^2>=4ab.
Donc a+b>=2Vab.==>(*) Si a et b sont positifs.
En utilisant *, on prend a=(1+a/b)^n et b=(1+b/a)^n.
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .==>(a)
D'autre part, en utilisant *, on prend a=1 et b=a/b.
Donc 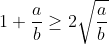$Deux exercices Gif$ .
Donc $Deux exercices Gif$ .==>(1)
De même $Deux exercices Gif$ .==>(2)
En multipliant 1 et 2, on obtient $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .
Donc $Deux exercices Gif$ .==>(b)
Et de a et b, on conclut que $Deux exercices Gif$ .
CQFD.

Bien, mais ce n'est que la première, et c'est la plus facile.
Je sais que c'est un peu difficile pour vous, mais pensez à utiliser des inégalités connus pour les autres inégalités(Tchebychev, Jensen, IAG ...)

Sujet: Re: Deux exercices Ven 19 Mar 2010, 15:14

Je propose quelques solutions que je vois maintenant pour le problem:
Methode 1 (Am-Gm 2 fois):
(1+a/b)^n + (1+b/a)^n>=[2(a/b)]^{n/2} + [2(b/a)]^{n/2}>=2^{n+1}
Methode 2 (Am-Gm 2 fois):
(1+a/b)^n + (1+b/a)^n >= 2[(1+a/b)(1+b/a)]^{n/2}>=2[2V(a/b)*2V(b/a)]^{n/2}=2^{n+1}
Methode 3 (Am-Gm + Cauchy-Schwarz):
(1+a/b)^n + (1+b/a)^n >= 2[(1+a/b)(1+b/a)]^{n/2}>=2[(1+V[(a/b)*(b/a)])^2]^{n/2}=2^{n+1}
Methode 3 (Jensen + Am-Gm):
considerons la fonction f(x)=x^n, cette fonction est bien convexe, d'où:
(1+a/b)^n + (1+b/a)^n >= 2[1/2(2+a/b+b/a)]^n>=2^{n+1}
Methode 4 (Hölder): on pose x=1+a/b et y=1+b/a, alors x+y>=4
(x^n+y^n)*2^{n-1}>= (x+y)^n>=2^{2n} d'ou x^n+y^n>=2^{n-1}
Methode 5 (Reccurence): Puisque l'inégalité est symetrique on suppose que a>=b et ainsi x>=y, pour n=0 l'inégalité est vérfié, en supposant que l'inégalité est verifié pour un entier n, on a d'après chebychev, x^{n+1} + y^{n+1}>= 1/2 (x+y)(x^n+y^n)>=2^{n+2} et par suite l'inégalité est verifié pour tous n£IN.
Methode 6 (Hölder):
(1+a/b)^n + (1+b/a)^n = (a+b)^n(1/a^n + 1/b^n)>=2^{n+1}
Methode 7 (Jensen):
considerons la fonction f(x)=(1+x)^n, cette dernière est bien convexe et croissante, et ainsi f(a/b)+f(b/a) = (1+a/b)^n + (1+b/a)^n >= 2f[(a/b + b/a)/2]>=2f(1)=2^{n+1}
Methode 8 (avec une lemme):
D'après la lemme (1+x)^n + (1+y)^n>= 2(1+xy)^{n}, on verifie directement le resultats voulu.
Methode 9 (Chebychev):
puisque l'inégalité est symetrique, on suppose que a>=b, alors: P(n) = (1+a/b)^n + (1+b/a)^n>= 1/2(2+a/b+b/a)((1+a/b)^{n-1} + (1+b/a)^{n-1}))>=2[(1 + a/b)^{n-1} + (1 + b/a)^{n-1}]=2P(n-1), en repetant l'operations plusieurs fois on trouve que: P(n)>=2P(n-1)>=4P(n-2)>=...>=2^n*P(0)=2^{n+1}.
Methode 10 (Cauchy Schwarz):
on pose a/b=x alors b/a = 1/x, et alors,
P(n)=(1+x)^n + (1+1/x)^n= (1+x)^n + [(x+1)/x]^n
P(n)= [(x²+x)^n + (x+1)^n]/x^n >=[2((x²+x)(1+x))^{n/2)]/x^n >= [2(x+x)^n]/[x^n]=2^{n+1}. CQFD

Dans toutes les methodes cités ci-dessus, l'égalité n'est verifié que si et seulement si a=b. Je vous propose un problème qui est très connu comme inégalité:
Problème:
Pour tous a,b,c>=0 tels que (a+b)(b+c)(c+a) =/= 0, Prouver que: a/(b+c) + b/(a+c) + c/(a+b) >= 3/2.

Sujet: Re: Deux exercices Ven 19 Mar 2010, 21:47

Un Chebyshev et un Am-Gm deux fois suffisent.
Si vous voulez la démo, je la posterai.

Sujet: Re: Deux exercices Dim 21 Mar 2010, 11:37

nmo a écrit:: Prends b=1 et a=1000.
Ce qui est en rouge est faux.
L'autre inégalité qui la suit est fausse.

Ouii )) mais bon voici une autre sans :

Premiérement on a : (a+b)^n>a^n+b^n (1) puisque (a,b >0) alors : 4^n>2^n+1
On a : ((a/b+1))^n>=2^n et ((b/a+1))^n>=2^n
Donc : ((a/b+1))^n((b/a+1))^n>=4^n
Donc : 2V((a/b+1)^n((b/a+1)^n>=4^n>=2^n+1 (car : 2^n*2^n>=2^n+1)
de méme on a : ((1+a/b))^n + ((1+b/a))^n>= 2V((a/b+1)^n((b/a+1)^n ( d'aprés a+b>=2Vab (a,b>0) )
Dont le résultat ^^

» Deux exercices..........!!
» Deux exercices de reccurence
» deux exercices de reccurence svp c'est urgent
» Deux exercices du livres du maths:
» Aide sur deux exercices de logique