| | Aide sur deux exercices de logique |  |
|
|
| Auteur | Message |
|---|
konica
Maître
 Nombre de messages : 141
Age : 28
Localisation : Tétouan
Date d'inscription : 19/03/2011
| | Sujet: Aide sur deux exercices de logique Sam 27 Aoû 2011, 14:04 | |
| Salut! Je suis bloqué sur deux exercices de logique, veuillez m'aider SVP  ! Exercice 1 : Soit x et y et z des nombres réels, l'un de ses nombres est égale à 0, et les deux autres ne le sont pas mais l'un est positif alors que l'autre est négatif. Supposons que toutes les trois assertions sont justes:    Comparer x et y et z. Exercice 2 : Montrer par récurrence quel que soit  et quel que soit les nombres réels strictement positifs  on a :  | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Aide sur deux exercices de logique Sam 27 Aoû 2011, 16:26 | |
| Exercice 1: Exercice 6 ici: https://mathsmaroc.jeun.fr/t18238-serie-d-exos-logiqueExercice 2: Soient a_1, a_2, ... , a_n des réels strictement positifs. Par récurrence sur n, montrons que: :\;&space;\;&space;\left&space;(&space;\sum_{i=1}^n&space;a_i&space;\right&space;)\left&space;(\sum_{i=1}^n&space;\frac{1}{a_i}&space;\right&space;)\geq&space;n^2) . Initialisation: pour n=1, on a: \left&space;(\sum_{i=1}^1\frac{1}{a_i}&space;\right&space;)\geq&space;1^2\Leftrightarrow&space;a_1\times&space;\frac{1}{a_1}\geq&space;1\Leftrightarrow&space;1\geq&space;1) , ce qui est vrai. Pour n=2, on a: \left&space;(\sum_{i=1}^2&space;\frac{1}{a_i}&space;\right&space;)\geq&space;2^2\Leftrightarrow&space;\left&space;(a_1+a_2&space;\right&space;)\left&space;(\frac{1}{a_1}+\frac{1}{a_2}&space;\right&space;)\geq&space;4) ^2}{a_1a_2}\geq&space;0) , ce qui est clairement vrai. Donc la relation qu'on veut démontrer est vérifiée pour l'indice n=1 et n=2. Hérédité: Soit 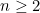 , on suppose que: \left&space;(\sum_{i=1}^n&space;\frac{1}{a_i}&space;\right&space;)\geq&space;n^2) , Et on montre que: \left&space;(\sum_{i=1}^{n+1}\frac{1}{a_i}&space;\right&space;)\geq&space;(n+1)^2) . Donc il suffit montrer que: \left&space;(\sum_{i=1}^n\frac{1}{a_i}+\frac{1}{a_{n+1}}&space;\right&space;)\geq&space;n^2+2n+1) . \left&space;(&space;\sum_{i=1}^{n}\frac{1}{a_i&space;}&space;\right&space;)+\frac{1}{a_{n+1}}\left&space;(&space;\sum_{i=1}^{n}&space;a_i\right&space;)+a_{n+1}\left&space;(&space;\sum&space;_{i=1}^{n}&space;\frac{1}{a_{i}}\right&space;)+a_{n+1}\times&space;\frac{1}{a_{n+1}}\geq&space;n^2+2n+1) . \left&space;(&space;\sum_{i=1}^{n}\frac{1}{a_i&space;}&space;\right&space;)+\frac{1}{a_{n+1}}\left&space;(&space;\sum_{i=1}^{n}&space;a_i\right&space;)+a_{n+1}\left&space;(&space;\sum&space;_{i=1}^{n}&space;\frac{1}{a_{i}}\right&space;)+1\geq&space;n^2+2n+1) . \left&space;(&space;\sum_{i=1}^{n}\frac{1}{a_i&space;}&space;\right&space;)+\frac{1}{a_{n+1}}\left&space;(&space;\sum_{i=1}^{n}&space;a_i\right&space;)+a_{n+1}\left&space;(&space;\sum&space;_{i=1}^{n}&space;\frac{1}{a_{i}}\right&space;)\geq&space;n^2+2n) . Et d'après notre supposition, on a: , donc pour montrer l'inégalité proposée, il suffit de montrer que: +a_{n+1}\left&space;(&space;\sum&space;_{i=1}^{n}&space;\frac{1}{a_{i}}\right&space;)\geq&space;2n) . +a_{n+1}\left&space;(&space;\frac{1}{a_1}+\frac{1}{a_2}+&space;\dots&space;+\frac{1}{a_n}\right&space;)\geq&space;2n) . &space;+(\frac{a_{n+1}}{a_1}+\frac{a_{n+1}}{a_2}+&space;\dots&space;+\frac{a_{n+1}}{a_n})\geq&space;2n) . +(\frac{a_{2}}{a_{n+1}}+\frac{a_{n+1}}{a_2})+&space;\dots&space;+&space;(\frac{a_n}{a_{n+1}}+\frac{a_{n+1}}{a_n})\geq&space;\underset{n&space;\;&space;\;&space;\mathrm{fois}}{\underbrace{{}2+2+&space;\dots&space;+&space;2}}) . +(\frac{a_{2}}{a_{n+1}}+\frac{a_{n+1}}{a_2}-2)+&space;\dots&space;+&space;(\frac{a_n}{a_{n+1}}+\frac{a_{n+1}}{a_n}-2)\geq&space;0) . +(\frac{a_{2}^2+a_{n+1}^2-2a_2a_{n+1}}{a_2a_{n+1}})+&space;\dots&space;+&space;(\frac{a_n^2+a_{n+1}^2-2a_na_{n+1}}{a_na_{n+1}})\geq&space;0) . ^2}{a_1a_{n+1}}+\frac{(a_2-a_{n+1})^2}{a_2a_{n+1}}+&space;\dots&space;+&space;\frac{(a_n-a{n+1})^2}{a_na_{n+1}}\geq&space;0) . Ce qui est vrai, donc la relation de récurrence est vérifiée pour le rang n+1, on conclut q'elle est aussi vraie pour le rang n. Synthèse de la récurrence: . | |
|
| | |
konica
Maître
Nombre de messages : 141
Age : 28
Localisation : Tétouan
Date d'inscription : 19/03/2011
| | Sujet: Re: Aide sur deux exercices de logique Mar 04 Oct 2011, 12:23 | |
| Wéé! Mais pourquoi tu as vérifié pour n=1 et n=2?? Et après t'as pris n>2??
Ce n'était pas suffisant de prendre n=1 pour l'initialisation? | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Aide sur deux exercices de logique Mar 04 Oct 2011, 19:24 | |
| J'ai vérifié que la propriété est vraie pour n=2, car j'ai cru que je vais l'utiliser pour montrer que la propriété est vraie pour n+1, donc, on peut éviter cette étape.
Mais en tous cas, ma réponse reste juste.
| |
|
| | |
konica
Maître
Nombre de messages : 141
Age : 28
Localisation : Tétouan
Date d'inscription : 19/03/2011
| | Sujet: Re: Aide sur deux exercices de logique Mer 05 Oct 2011, 11:58 | |
| | |
|
| | |
diablo902
Maître
Nombre de messages : 279
Age : 26
Date d'inscription : 01/07/2011
| | Sujet: Re: Aide sur deux exercices de logique Jeu 22 Déc 2011, 10:57 | |
| L'exercice 2 n'est pas une application directe du Caushy Shwarz  | |
|
| | |
momo1729
Maître
Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
| | Sujet: Re: Aide sur deux exercices de logique Jeu 22 Déc 2011, 12:25 | |
| Pourquoi pas ?
C'est une application triviale. | |
|
| | |
konica
Maître
Nombre de messages : 141
Age : 28
Localisation : Tétouan
Date d'inscription : 19/03/2011
| | Sujet: Re: Aide sur deux exercices de logique Jeu 22 Déc 2011, 18:29 | |
| Ouais! Mais j'ai voulu la méthode de récurrence.....  | |
|
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
| | Sujet: Re: Aide sur deux exercices de logique Dim 17 Mar 2013, 11:05 | |
| On peut la résoudre avec AM-GM | |
|
| | |
Wissal El
Féru
 Nombre de messages : 62
Age : 27
Localisation : Sefrou
Date d'inscription : 16/12/2012
| | Sujet: Re: Aide sur deux exercices de logique Dim 17 Mar 2013, 12:55 | |
| Et d'après notre supposition, on a: , donc pour montrer l'inégalité proposée, il suffit de montrer que: . Salut , J pense qu'Ici on n'a qu'une implication ; on a perdu l'équivalence .  | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Aide sur deux exercices de logique | |
| |
|
| | |
| | Aide sur deux exercices de logique | |
|
