| | Autre défi: |  |
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Autre défi: Sujet: Autre défi:  Jeu 14 Jan 2010, 16:38 Jeu 14 Jan 2010, 16:38 | |
| a,b, et c sont des réels tels que pour tout x de R on a
[ax^2+bx+c]=<1.
1/Montrez que: [c]=<1.
2/Montrez que: [a+c]=<1.
3/Déduisez que a^2+b^2+c^2=<5.
Bonne chance.
P.S:[] veut dire la valeur absolue. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Jeu 14 Jan 2010, 19:31 Jeu 14 Jan 2010, 19:31 | |
| On fixe x=0 on aura |c| ≤1
On fixe x=1 puis x=-1 ca donne :
|a+b+c|≤1 et |a-b+c|≤1
-1≤a+b+c≤1 et -1≤a-b+c≤1
On somme et on divise sur 2 ca donnerai :
-1≤a+c≤1
résultat voulu.. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Jeu 14 Jan 2010, 20:01 Jeu 14 Jan 2010, 20:01 | |
| 3/ %20\leq%201) %20\leq%201) En sommant, cela donne : )+(a^{2}+b^{2}+c^{2}+2(ac+ab+bc))%20\leq%202%20\\%20\Rightarrow%20a^{2}+b^{2}+c^{2}%20\leq%201-2ac) (1) On a par ailleurs que 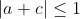 et 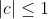 D'où 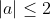 Il est facile alors de déduire que 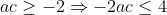 Par transitivité, (1) implique le résultat escompté. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 13:17 Dim 17 Jan 2010, 13:17 | |
| Je ne comprends pas comment tu as eu que [a]=<2.
Si on a [a]=<2 et [c]=<1.
On trouve [a+c]=<3.
Ce qui est faux.
Et merci pour ta réponse. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 13:38 Dim 17 Jan 2010, 13:38 | |
| | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 13:44 Dim 17 Jan 2010, 13:44 | |
| Une fonction de 2éme degré ne peut pas avoir un maximum et minimum en même temps  Enfin je crois que c'est pour tous x£[-1;1] | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 14:34 Dim 17 Jan 2010, 14:34 | |
| Il y'a un autre exo semblable à celui là :
Soit x £ [-1;1]
MQ si |ax²+bx+c|<=1 alors |cx²+bx+a|<=1 | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 14:46 Dim 17 Jan 2010, 14:46 | |
| - Sylphaen a écrit:
- Il y'a un autre exo semblable à celui là :
Soit x £ [-1;1]
MQ si |ax²+bx+c|<=1 alors |cx²+bx+a|<=1 je crois que c plutôt . |cx²+bx+a|=<2 un ancien problème de la semaine  | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 15:06 Dim 17 Jan 2010, 15:06 | |
| Lol je me demandais aussi car j'ai trouvé 2 et sur le livre il y'a 1 ^^
Merci :d | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 18:58 Dim 17 Jan 2010, 18:58 | |
| | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 19:01 Dim 17 Jan 2010, 19:01 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 19:15 Dim 17 Jan 2010, 19:15 | |
| - Sylphaen a écrit:
- Oui Mais si a#0 donc ..
Si 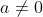 , la condition 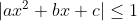 n'est pas satisfaite. D'où 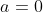 | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 20:09 Dim 17 Jan 2010, 20:09 | |
| Ben alors c'est le même cas pour b .. car une fonction affine n'a pas de limite xD | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Dim 17 Jan 2010, 21:06 Dim 17 Jan 2010, 21:06 | |
| - Sylphaen a écrit:
- Ben alors c'est le même cas pour b .. car une fonction affine n'a pas de limite xD
D'où 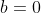 Une fois que ces précisions sont établies, le problème devient tout à coup trivial. La condition initiale devient 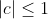 Le maximum de 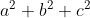 vaut alors 1. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  Ven 22 Jan 2010, 18:21 Ven 22 Jan 2010, 18:21 | |
| - majdouline a écrit:
- Sylphaen a écrit:
- Il y'a un autre exo semblable à celui là :
Soit x £ [-1;1]
MQ si |ax²+bx+c|<=1 alors |cx²+bx+a|<=1 je crois que c plutôt . |cx²+bx+a|=<2
un ancien problème de la semaine  Pouvez vous m'indiquer le lien s'il vous plait. Et merci pour les réponses. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Autre défi: Sujet: Re: Autre défi:  | |
| |
|
  | |
| | Autre défi: |  |
|
