derivée premiere

Bonjour la 2éme question me pose probléme

Trois fonctions f , g et h sont derivables sur [ 0 , + l'infini[ , elles sont représentées par les courbes C1 ,C2, C3 mais dans le desordre
On sait que la fonction h est la derivée de g et que g est la derivée de f
1) retrouver leurs courbes représentatives , en expliquant
2) La fonction f est de la forme f(x) = ax + b + c / x+1 . Sachant que f(0) = 0 , f(2) = 4 et la fonction f admet un maximum , etablir trois equations d'inconnues a , b et c
Résoudre le systéme et en deduire l'expression f(x)

pour la question 1 'est fait mais la question 2 me pose probléme je n'arrive pas a trouver le 3éme systéme

f(0) = 0 --> f(0) = (b+c)/1 -> (b+c)/1 = 0
f(2)=4 --> (2a+b+c)/3 = 4

salam

on voit pas les courbes ?????

.

pour traduire le maximum

f'(x) doit s'annuler en un point xo

.

bonsoir alyssa

il y'a une faute dans votre ennonce f peut etre definie ainsi:

f(x) = ax + b + (c/(x+1))

f(0) = 0==> c=-b
f(2) = 4 ===> b= 6 - 3a
f'(.) = 0 ==> ...
donc c= -b = 3a-6

alors il faut determiner le point ou f admet son maximum c a d ou f'( . ) = 0

alors g peut definir comme :

g(x) = a x²/2 + bx + c ln(x+1) + β

β est une constante reelle
et
h(x) = (a/6) x^3 + (b/2) x² + c (x+1)ln(x+1) + (β-c)x -c + λ

λ est une constante

je n'est rien compris nan mais la question 1 je l'est fait donc pas besoin des coubres

au passage je suis en premiere ce que vous me dites la je ne comprend pas

alyssa a écrit:

au passage je suis en premiere ce que vous me dites la je ne comprend pas

BSR alyssa !!

Je comprends fort bien qu'étant en Première ( du Système Français ) Tu n'aies pas compris les propositions des Forumistes intervenants .
Je pense que celà vient de deux choses :

1) Nous aurions besoin de voir les courbes C1 ,C2 et C3 et surtout celle qui correspond au graphe de g puisque la Dérivée de f est g !!!!!!!!!!
Dire que f admet un MAXIMUM celà revient à voir ou g s'annulle ????

2) Ton écriture f(x) = ax + b + c / x+1 est un peu CONFUSE !
S'agit-il de f(x) = {ax + b + c} / {x+1}
ou bien de f(x) = ax + b + {c / x+1}
Il faut prendre toujours soin de mettre des parenthèses pour fixer les priorités dans les Opérations .....

LHASSANE

dsl mais je met ce qu'il y a sur l'enoncé , et il n'y a pas de parenthese

voila les courbes

http://www.zimagez.com/zimage/hebergeurdimage.php

alyssa a écrit:

voila les courbes

http://www.zimagez.com/zimage/hebergeurdimage.php

BJR alyssa !!

Maintenant , on peut te répondre sans hésitations ......
Le graphe de f c'est la courbe (C2)
Le graphe de f'=g c'est la courbe (C3)
et donc celui de f"=g'=h est ( C1)

On voit alors en examinant (C2) que f admet un MAXIMUM au poit xo=2 et qui vaut f(2)=4 et que f' =g s'annulle bien pour xo=2 .
On cherche alors pour f une expression du type :
f(x)=a.x+b+(c/(x+1))

Les conditions f(0)=0 et f(2)=4 te donnent les deux relations :
b+c=0 et 2.a+b+(c/3)=4
Il te reste à exprimer que f'(2)=g(2)=0
Or g(x)=f'(x)= a - (c/(x+1)^2))
et donc g(2)=a-(c/9)
On doit donc avoir aussi a-(c/9)=0
Ton système final sera :
b+c=0
2.a+b+(c/3)=4
a=c/9
qui se résoud sans difficultés :
On aura b=-c et a=c/9 on remplace tout celà dans la 2ème équation pour trouver :
(2.c)/9 -c +(c/3)=4 c'est à dire (2.c-9.c+3.c)/9=4 d'ou c=-9
Ainsi a=-1 , b=9 et c=-9

CONCLUSION : on a f(x)=-x+9 -(9/(x+1)) pour tout x dans ]0;+oo[ .

LHASSANE

Oeil_de_Lynx a écrit:

alyssa a écrit:

voila les courbes

http://www.zimagez.com/zimage/hebergeurdimage.php

BJR alyssa !!

Maintenant , on peut te répondre sans hésitations ......
Le graphe de f c'est la courbe (C2)
Le graphe de f'=g c'est la courbe (C3)
et donc celui de f"=g'=h est ( C1)

On voit alors en examinant (C2) que f admet un MAXIMUM au poit xo=2 et qui vaut f(2)=4 et que f' =g s'annulle bien pour xo=2 .
On cherche alors pour f une expression du type :
f(x)=a.x+b+(c/(x+1))

Les conditions f(0)=0 et f(2)=4 te donnent les deux relations :
b+c=0 et 2.a+b+(c/3)=4
Il te reste à exprimer que f'(2)=g(2)=0
Or g(x)=f'(x)= a - (c/(x+1)^2))
et donc g(2)=a-(c/9)
On doit donc avoir aussi a-(c/9)=0
Ton système final sera :
b+c=0
2.a+b+(c/3)=4
a=c/9
qui se résoud sans difficultés :
On aura b=-c et a=c/9 on remplace tout celà dans la 2ème équation pour trouver :
(2.c)/9 -c +(c/3)=4 c'est à dire (2.c-9.c+3.c)/9=4 d'ou c=-9
Ainsi a=-1 , b=9 et c=-9

CONCLUSION : on a f(x)=-x+9 -(9/(x+1)) pour tout x dans ]0;+oo[ .

LHASSANE

b+c=0 et f(2) = 4 ==) a= 6

==) f(x) = 6x /(x+1).

BJR {}{}=l'infini !!

Tu devrais jeter un COUP d'OEIL avisé sur l'énoncé d'une part :

alyssa a écrit:

.........

Trois fonctions f , g et h sont derivables sur [ 0 , + l'infini[ , elles sont représentées par les courbes C1 ,C2, C3 mais dans le desordre
On sait que la fonction h est la derivée de g et que g est la derivée de f
1) retrouver leurs courbes représentatives , en expliquant
2) La fonction f est de la forme f(x) = ax + b + c / x+1 . Sachant que f(0) = 0 , f(2) = 4 et la fonction f admet un maximum , etablir trois equations d'inconnues a , b et c
Résoudre le systéme et en deduire l'expression f(x)

pour la question 1 'est fait mais la question 2 me pose probléme je n'arrive pas a trouver le 3éme systéme

f(0) = 0 --> f(0) = (b+c)/1 -> (b+c)/1 = 0
f(2)=4 --> (2a+b+c)/3 = 4

car il y a une erreur : f(2)=2.a+b+(c/3) au lieu de (2a+b+c)/3 .
alyssa a fait une ERREUR !!!!!!

puis , d'autre part , sur les courbes (C1) , (C2) et (C3)

alyssa a écrit:

voila les courbes

http://www.zimagez.com/zimage/hebergeurdimage.php

LHASSANE

non je n'est pas fait d'erreur sur l'énoncé c'est marquer comme ca il n' y a ni parentheses ni rien

oui c'est certain , parce que dans l'exercice il ya un vrai trait de fraction comme ça :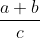
et pas seulement un slash comme ceci : a+b/c dans ce cas il faut ecrire (a+b)/c
alors que quand toi tu ecris a+b/c on peut l'interpreter aussi comme ça : .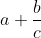

Alors pour différencier il faudrait que toi tu introduises des parentheses ...