| | Première étape olympiades de première 15-11-2013 |  |
|
|
| Auteur | Message |
|---|
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Première étape olympiades de première 15-11-2013 Sujet: Première étape olympiades de première 15-11-2013  Ven 15 Nov 2013, 19:26 Ven 15 Nov 2013, 19:26 | |
| Exercice 1 (AUS): Exercice 2 (BMO): Exercice 2 (BMO): Exercice 3 (BMO): Exercice 3 (BMO):soient a,b et c les trois longueurs de côtés d'un triangle. Sachant que  déterminer la plus grande aire possible de ce triangle. Exercice 4 (SAMC):soit ABC un triangle. D et E deux points appartenant respectivement aux côtés [BC] et [AC] du triangle et tel que  . Le cercle circonscrit au triangle ABD rencontre le segment [BE] au point F (distinct de B). La demi-droite [AF) coupe le segment [DE] au point P. Montrer que 
Dernière édition par legend-crush le Sam 16 Nov 2013, 12:05, édité 1 fois | |
|
  | |
Nas8
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 28
Date d'inscription : 26/11/2011
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Ven 15 Nov 2013, 20:15 Ven 15 Nov 2013, 20:15 | |
| Soit x1 = x2 donc 0 =1 impossible
Soit x1 > x2 donc x1 = x2 +1
D'apres le theoreme de Viete on a -p = x1 + x2 = 2.x2 + 1 et q = x1.x2 = x²2 +x2
donc lq-pl = lx²2 + 3x2 +1l = 1
Si x2 est un entier p et q et x1 sont automatiquement des entiers
- pour -3-v5<2.x2<-3+v5 on a x2 = 1 ou x2 = 2
- pour 2.x2 < -3-v5 ou -3+v5 < 2x2 on a x2 = 0 ou x2 = -3
Conclusion p et q et x1 et x2 sont des entiers relatifs
| |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Ven 15 Nov 2013, 22:16 Ven 15 Nov 2013, 22:16 | |
|  on s'assure ensuite que le triplet (1,2,3) est bel et bien une solution du système, donc S={(1,2,3)} | |
|
  | |
Nas8
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 28
Date d'inscription : 26/11/2011
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Ven 15 Nov 2013, 22:44 Ven 15 Nov 2013, 22:44 | |
| ah c'est le meme exercice de géométrie pour les 2éme années | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 11:55 Sam 16 Nov 2013, 11:55 | |
| Combien avez-vous trouver f le troisième exercice? | |
|
  | |
Zouhair-Evariste
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 27
Date d'inscription : 31/08/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 12:35 Sam 16 Nov 2013, 12:35 | |
| 1/ j'ai trouvé 4 solutions de la forme (x_1,x_2,p,q), et dans tout les cas x_1,x_2,p,q sont des entiers relatifs
2/ x=1, y=2et z=3
3/ Formule de Héron + inégalité triangulaire j'ai trouvé 6rac(3) comme résultat | |
|
  | |
Zouhair-Evariste
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 27
Date d'inscription : 31/08/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 12:44 Sam 16 Nov 2013, 12:44 | |
| - Nas8 a écrit:
- Soit x1 = x2 donc 0 =1 impossible
Soit x1 > x2 donc x1 = x2 +1
D'apres le theoreme de Viete on a -p = x1 + x2 = 2.x2 + 1 et q = x1.x2 = x²2 +x2
donc lq-pl = lx²2 + 3x2 +1l = 1
Si x2 est un entier p et q et x1 sont automatiquement des entiers
- pour -3-v5<2.x2<-3+v5 on a x2 = 1 ou x2 = 2
- pour 2.x2 < -3-v5 ou -3+v5 < 2x2 on a x2 = 0 ou x2 = -3
Conclusion p et q et x1 et x2 sont des entiers relatifs
pour faciliter les choses l'equation en rouge se résume en deux cas cas1/ x²_1+3x_1+1=1 alors x_1=0 ou x_3=3 cas2/ x²_1+3x_1+1=-1 alors x_1=-1 ou x_3=-2 sachant que x_2=x_1+1 (par symétrie de rôle j'ai posé x1<x2) on trouve facilement x2 p et q | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 12:58 Sam 16 Nov 2013, 12:58 | |
| - Zouhair-Evariste a écrit:
- 1/ j'ai trouvé 4 solutions de la forme (x_1,x_2,p,q), et dans tout les cas x_1,x_2,p,q sont des entiers relatifs
2/ x=1, y=2et z=3
3/ Formule de Héron + inégalité triangulaire j'ai trouvé 6rac(3) comme résultat Faudrait t'assurer qu'il existe bel et bien un a<2 et un b<3 et un c<4 pour lequel A=6rac(3) ce qui est faux je crois. pour moi, j'ai dit que l'aire est maximale lorseque a=2 et b=3 et c=4 et en utilisant la formule de Héron j'ai trouvé 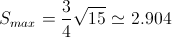 mais je suis pas sur de cette démarche | |
|
  | |
Zouhair-Evariste
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 27
Date d'inscription : 31/08/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 13:14 Sam 16 Nov 2013, 13:14 | |
| voici ma l'exercice le pour le 3 : on a<b+c donc a-b<c alors a-b+c<2c sachant que c<2 on a a-b+c<4
du meme maniére j'ai trouvé la valeur max de a+b-c et a-b+c et pour a+b+c il est facile de trouver que 9 est son max | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 13:32 Sam 16 Nov 2013, 13:32 | |
| - Zouhair-Evariste a écrit:
- voici ma l'exercice le pour le 3 : on a<b+c donc a-b<c alors a-b+c<2c sachant que c<2 on a a-b+c<4
du meme maniére j'ai trouvé la valeur max de a+b-c et a-b+c et pour a+b+c il est facile de trouver que 9 est son max ce passage est faux je crois et en plus l'aire du triangle ne peut en aucun cas etre supérieur à 3 et voila pourquoi :  | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 13:59 Sam 16 Nov 2013, 13:59 | |
| La vraie réponse est en fait A=3 et c'est lee cas où a=2 et b=3 et c= rac(13)<4 | |
|
  | |
Zouhair-Evariste
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 27
Date d'inscription : 31/08/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 14:07 Sam 16 Nov 2013, 14:07 | |
| - legend-crush a écrit:
- La vraie réponse est en fait A=3 et c'est lee cas où a=2 et b=3 et c= rac(13)<4
je crois que c'est correct | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 14:49 Sam 16 Nov 2013, 14:49 | |
| S'il vous, quel est le nombre minimal pour etre qualifié à l'examen suivant
| |
|
  | |
Zouhair-Evariste
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 27
Date d'inscription : 31/08/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 15:30 Sam 16 Nov 2013, 15:30 | |
| - legend-crush a écrit:
- S'il vous, quel est le nombre minimal pour etre qualifié à l'examen suivant
tout les eleves qui ont participé au premier test sont invité a passé le 2eme | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 17:32 Sam 16 Nov 2013, 17:32 | |
| | |
|
  | |
Zouhair-Evariste
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 27
Date d'inscription : 31/08/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 17:38 Sam 16 Nov 2013, 17:38 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 19:08 Sam 16 Nov 2013, 19:08 | |
| Et comment sais-tu que tout le monde passera le deuxième examen | |
|
  | |
Zouhair-Evariste
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 27
Date d'inscription : 31/08/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 19:41 Sam 16 Nov 2013, 19:41 | |
| oh !! pardon ce sont les élèves du bac qui ont ce système !
en ce qui concerne 1ere bac, prend la dernière page de ce document http://www.men.gov.ma/SiteCollectionDocuments/crp13491131009.pdf | |
|
  | |
Nas8
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 28
Date d'inscription : 26/11/2011
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Sam 16 Nov 2013, 22:03 Sam 16 Nov 2013, 22:03 | |
| Les olympiades de premiére année sont un peu différents des precedantes années , vous passez 2 examan pour etre qualifié au prochaine etape qui contient elle aussi 2 autres et se faire selectionné parmi les eleves pour les 2 derniérs . | |
|
  | |
Arthur Holmes
Débutant

 Nombre de messages : 2 Nombre de messages : 2
Age : 27
Localisation : Mohammedia
Date d'inscription : 18/11/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Lun 18 Nov 2013, 12:42 Lun 18 Nov 2013, 12:42 | |
| en ce qui concerne le 3ème exercice, j'ai pris la plus grande mesure de chaque côté du triangle, ensuite j'ai appliqué le théorème d'Al Kashi pour obtenir l'angle formé entre deux côtés ( ex : b et c ), et après j'ai utilisé cette règle : Aire du triangle = (1/2).b.c.sin(l'angle compris entre ces deux côtés) et j'ai obtenus Aire maximale du triangle égale à à peu près 3 ! qu'en pensez-vous ? | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Mar 19 Nov 2013, 20:54 Mar 19 Nov 2013, 20:54 | |
| Ma méthode pour le 3:
On pose h1 une hauteur du triangle, qui divise un angle du triangle en deux, notons alpha et beta.
L'on a S = h1 x c /2 = cos(alpha)xaxc/2.
Cos(alpha) <= 1. L'égalité se fait dans alpha = 90¤
de même on trouve deux autres valeurs pour S, et on choisit la plus grande.
On trouve Smax = 6. | |
|
  | |
Zouhair-Evariste
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 27
Date d'inscription : 31/08/2013
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  Mar 19 Nov 2013, 21:08 Mar 19 Nov 2013, 21:08 | |
| - Sketshup a écrit:
- Ma méthode pour le 3:
On pose h1 une hauteur du triangle, qui divise un angle du triangle en deux, notons alpha et beta.
L'on a S = h1 x c /2 = cos(alpha)xaxc/2.
Cos(alpha) <= 1. L'égalité se fait dans alpha = 90¤
de même on trouve deux autres valeurs pour S, et on choisit la plus grande.
On trouve Smax = 6. t'as dit que Smax=6, alors faut il trouver un triple (a;b;c) qui vérifie cette surface tout en respectant la condition !!! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Première étape olympiades de première 15-11-2013 Sujet: Re: Première étape olympiades de première 15-11-2013  | |
| |
|
  | |
| | Première étape olympiades de première 15-11-2013 |  |
|
