| | Olympiade de première, deuxième étape, premier test: |  |
|
+4Humber Thelastmetalsong9 legend-crush nmo 8 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Olympiade de première, deuxième étape, premier test: Sujet: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 18:53 Ven 22 Fév 2013, 18:53 | |
| Je vous propose le test passé aujourd'hui (le 22 Février 2013): Exercice1: (MAR MC)Soient  ,  et  trois nombres réels vérifiant: 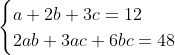 . Trouver  ,  et  . Exercice2: (MAR MC)Trouver toutes les fonctions polynomiales  vérifiant  : P(x+1)=P(x)+2x+1) . Exercice3: (MAR MC)Soient  et  deux réels positifs; Montrer que \bigg(\sqrt{\sqrt{64a}+\sqrt{64b}}\bigg)-\sqrt{2}) Exercice4: (BLR MC) Exercice4: (BLR MC)Soit 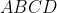 un quadrilatère inscriptible (inscrit dans un cercle) tel que 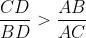 . Montrer que 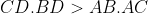 . Bonne chance.N.B: Trois exercices créés par la délégation marocaine...
Dernière édition par nmo le Ven 22 Fév 2013, 19:57, édité 3 fois | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 19:07 Ven 22 Fév 2013, 19:07 | |
| s'il vous plait c pour quand Les Tronc commun (Seconde)!!  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 19:12 Ven 22 Fév 2013, 19:12 | |
| - nmo a écrit:
- Exercice3: (MAR MC)
Soient  et et  deux réels positifs; Montrer que deux réels positifs; Montrer que \bigg(\sqrt{\sqrt{64a}+\sqrt{64b}}\bigg)-\sqrt{2}) . . L'inégalité à démontrer s'écrit (\sqrt{a}-\sqrt{b})\ge2\sqrt{2}(\sqrt{a}-\sqrt{b})\bigg(\sqrt{\sqrt{a}+\sqrt{b}}\bigg)-\sqrt{2}) . On simplifie par  qui dérange à première vue, on trouve (\sqrt{a}-\sqrt{b})+1\ge2(\sqrt{a}-\sqrt{b})\bigg(\sqrt{\sqrt{a}+\sqrt{b}}\bigg)) . Ce qui s'écrit encore ^2(\sqrt{a}+\sqrt{b})+1\ge2(\sqrt{a}-\sqrt{b})\bigg(\sqrt{\sqrt{a}+\sqrt{b}}\bigg)) . Qui n'est que l'inégalité arithmético-géométrique... Sauf erreurs! | |
|
  | |
Thelastmetalsong9
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 28
Localisation : xena planet
Date d'inscription : 09/11/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 19:21 Ven 22 Fév 2013, 19:21 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 19:30 Ven 22 Fév 2013, 19:30 | |
| - nmo a écrit:
- Exercice4: (BLR MC)
Soit 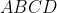 un quadrilatère inscriptible (inscrit dans un cercle) tel que un quadrilatère inscriptible (inscrit dans un cercle) tel que 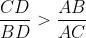 . .
Montrer que 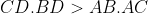 . . Soit 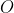 l'intersection des deux diagonales de ce quadrilatère. On a 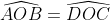 et 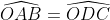 . Donc les deux triangles 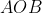 et 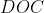 sont semblables, d'où: 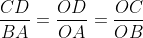 .==>(*) On pose désormais: 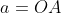 , 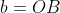 , 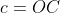 et 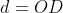 . L'inégalité à démontrer s'écrit: 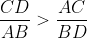 , ou encore 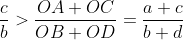 selon *. Soit 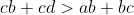 , ou encore 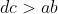 .==>(**) D'un autre coté, on a 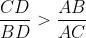 , soit 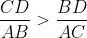 . Avec les notation introduite, ça devient 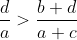 , en utilisant encore *. Ce qui donne: 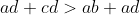 , ou bien 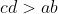 . Ce qui achève la démonstration. Sauf erreurs!
Dernière édition par nmo le Sam 23 Fév 2013, 18:15, édité 2 fois (Raison : Correction d'une erreur.) | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 | |
  | |
Thelastmetalsong9
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 28
Localisation : xena planet
Date d'inscription : 09/11/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 19:42 Ven 22 Fév 2013, 19:42 | |
| - nmo a écrit:
- nmo a écrit:
- Exercice4: (BLR MC)
Soit 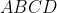 un quadrilatère inscriptible (inscrit dans un cercle) tel que un quadrilatère inscriptible (inscrit dans un cercle) tel que 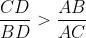 . .
Montrer que 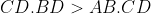 . . Soit 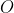 l'intersection des deux diagonales de ce quadrilatère. l'intersection des deux diagonales de ce quadrilatère.
On a 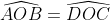 et et 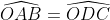 . .
Donc les deux triangles 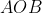 et et 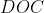 sont semblables, d'où: sont semblables, d'où: 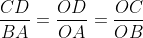 .==>(*) .==>(*)
On pose désormais: 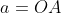 , , 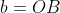 , , 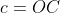 et et 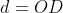 . .
L'inégalité à démontrer s'écrit: 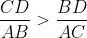 , ou encore , ou encore 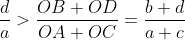 selon *. selon *.
Soit 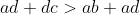 , ou encore , ou encore 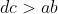 .==>(**) .==>(**)
D'un autre coté, on a 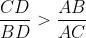 , soit , soit 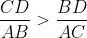 . .
Avec les notation introduite, ça devient 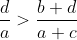 , en utilisant encore *. , en utilisant encore *.
Ce qui donne: 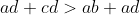 , ou bien , ou bien 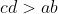 . .
Ce qui achève la démonstration.
Sauf erreurs! merci ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 19:46 Ven 22 Fév 2013, 19:46 | |
| - nmo a écrit:
- Exercice2: (MAR MC)
Trouver toutes les fonctions polynomiales  vérifiant vérifiant  : P(x+1)=P(x)+2x+1) . .
On introduit le polynôme  défini par:  : Q(x)=P(x)-x^2) . On a  : Q(x+1)=P(x+1)-(x+1)^2=P(x)+2x+1-x^2-2x-1) . Donc  : Q(x+1)=P(x)-x^2=Q(x)) . Il s'ensuit que  est constante; i.e:  : (\forall x\in\mathbb{R}):Q(x)=c) . Finalement:  : P(x)=x^2+c) avec c un réel connu. Sauf erreurs! | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 21:13 Ven 22 Fév 2013, 21:13 | |
|
Dernière édition par seledeur le Sam 25 Jan 2014, 20:40, édité 1 fois | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 21:45 Ven 22 Fév 2013, 21:45 | |
| Mr Seledeur pourquoi exactement x²,alors il suffit de conjecturer que P(x)=x² est Une solution et ensuite essayer si on ajoute une constante est ce que ça serai aussi une solution . c'est à dire voir que P(x)=x²+c est une solution . d'ou vient l'idée de Mr nmo - seledeur a écrit:
- J'ai montré que P est paire xD, j'aurai qq chose ?
Je crois que tu vas avoir un Zéro Zeroualien-Mat3échien-bourichien . Amicalement .
Dernière édition par alidos le Sam 23 Fév 2013, 00:29, édité 1 fois | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Ven 22 Fév 2013, 23:27 Ven 22 Fév 2013, 23:27 | |
| - alidos a écrit:
- il suffit de conjecturer que P(x)=x² est Une solution et ensuite essayer si
on ajoute une constante est ce que ça serai aussi une solution . c'est à dire voir que P(x)=x²+c
Amicalement . C'est faux comme démarche. | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 00:25 Sam 23 Fév 2013, 00:25 | |
| aLalalalalalalalala ..... a Mr Radouane_BNE
c'est pas une démarche Mr Radouane , c'est un passage pensif pour tracer le chemin
auquel on va attaquer l'exercice .
a partir de là on peut suivre la démarche de Mr nmo
j'ai voulu que expliquer a Mr seledeur ce qui nous a poussé pour prendre
Q(x)=P(x)-x² . | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 01:17 Sam 23 Fév 2013, 01:17 | |
| D'accord, il y'a juste un petit passage à montrer, si P polynome verifiant P(x+1)=P(x) pour tout x, alors P est constant.
On pose Q(X) = P(X) - P(0) alors Q(X+1) = P(X+1) - P(0) = P(X) - P(0) = Q(X)
De plus Q(0) = 0 donc Q(1) = 0 = Q(2) = Q(3)
Conjecture : Q(n) = 0
Soit P(n) la propriété " n , Q(n) = 0 "
* P(0) évident
* Soit n € N, supposons P(n) et montrons P(n+1) :
Q(n+1) = P(n+1) - P(0) = P(n) - P(0) = Q(n) = 0 donc P(n+1) vrai
Par récurrence, on déduit que pour n€N, Q(n) = 0
Donc Q admet une infinité de racine donc il est nul donc P(X) = P(0) ie. P constant | |
|
  | |
k.abdo
Féru

 Nombre de messages : 32 Nombre de messages : 32
Age : 28
Date d'inscription : 14/04/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 01:20 Sam 23 Fév 2013, 01:20 | |
| - Humber a écrit:
- Exercice 1 :
^2+(b-3c)^2+(3c-a)^2=0%20\end{aligned}%20\\\\%20\implies%20) CE PASSAGE : il y a un probléme verifier M. humber | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 01:28 Sam 23 Fév 2013, 01:28 | |
| Pour le 1ier exercice, on prend x=a/12, y=2*b/12 et z=3*c/12, le problème devient ainsi :
x+y+z=1,
xy+yz+zx=1/3,
Or on sait que 1=(x+y+z)^2=(x^2+y^2+z^2)+2*(xy+yz+zx) =>3(xy+yz+zx)=3, ce qui implique puisqu'on a égalité que x=y=z=1/3, finalement a=4,b=2 et c=4/3. | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 01:30 Sam 23 Fév 2013, 01:30 | |
| - radouane_BNE a écrit:
- D'accord, il y'a juste un petit passage à montrer, si P polynome verifiant P(x+1)=P(x) pour tout x, alors P est constant.
On pose Q(X) = P(X) - P(0) alors Q(X+1) = P(X+1) - P(0) = P(X) - P(0) = Q(X)
De plus Q(0) = 0 donc Q(1) = 0 = Q(2) = Q(3)
Conjecture : Q(n) = 0
Soit P(n) la propriété " n , Q(n) = 0 "
* P(0) évident
* Soit n € N, supposons P(n) et montrons P(n+1) :
Q(n+1) = P(n+1) - P(0) = P(n) - P(0) = Q(n) = 0 donc P(n+1) vrai
Par récurrence, on déduit que pour n€N, Q(n) = 0
Donc Q admet une infinité de racine donc il est nul donc P(X) = P(0) ie. P constant Effectivement Mr Radouane ,vu à la sévérité de la correction à qui j'ai assister au stage de rabat ,il faut absolument prouver ce passage pour souhaiter avoir les points complets de l'exercice . | |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 01:36 Sam 23 Fév 2013, 01:36 | |
| Pour le 2iem exercice, on pose a=x^2 et b=y^2. En divisant par 2 on se ramène après simplification à :
x^3-xy(x+y)+y^3 > 2(x-y)sqrt(x+y)-1, or x^3-xy(x+y)+y^3=(x+y)(x-y)^2, ainsi l'inégalité est équivalente à :
((x-y)*sqrt(x+y)-1)^2 >=0, ce qui est évidemment vrai. | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 01:50 Sam 23 Fév 2013, 01:50 | |
| - k.abdo a écrit:
- Humber a écrit:
- Exercice 1 :
^2+(b-3c)^2+(3c-a)^2=0%20\end{aligned}%20\\\\%20\implies%20a=2b=3c%20\implies%20S=%20\left%20{%204;2;\frac{4}{3}%20\right%20})
CE PASSAGE : il y a un probléme verifier M. humber Comment ? | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 06:36 Sam 23 Fév 2013, 06:36 | |
|
Dernière édition par seledeur le Sam 25 Jan 2014, 20:41, édité 2 fois | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 10:52 Sam 23 Fév 2013, 10:52 | |
| - nmo a écrit:
- nmo a écrit:
- Exercice4: (BLR MC)
Soit 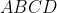 un quadrilatère inscriptible (inscrit dans un cercle) tel que un quadrilatère inscriptible (inscrit dans un cercle) tel que 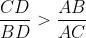 . .
Montrer que 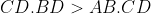 . . Soit 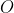 l'intersection des deux diagonales de ce quadrilatère. l'intersection des deux diagonales de ce quadrilatère.
On a 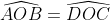 et et 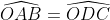 . .
Donc les deux triangles 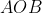 et et 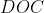 sont semblables, d'où: sont semblables, d'où: 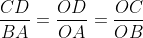 .==>(*) .==>(*)
On pose désormais: 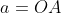 , , 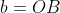 , , 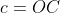 et et 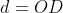 . .
L'inégalité à démontrer s'écrit: 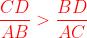 , ou encore , ou encore 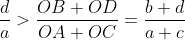 selon *. selon *.
Soit 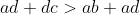 , ou encore , ou encore 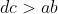 .==>(**) .==>(**)
D'un autre coté, on a  , soit , soit 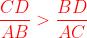 . .
Avec les notation introduite, ça devient 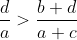 , en utilisant encore *. , en utilisant encore *.
Ce qui donne: 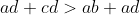 , ou bien , ou bien 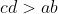 . .
Ce qui achève la démonstration.
Sauf erreurs! L"équivalence que vous avez faites est fausse à ce que je vois, pourriez vous réviser ce qui est en rouge ? | |
|
  | |
k.abdo
Féru

 Nombre de messages : 32 Nombre de messages : 32
Age : 28
Date d'inscription : 14/04/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 17:12 Sam 23 Fév 2013, 17:12 | |
| comment tu trouve l'éqoition :
(a-2b)²+(b-3c)²+(3c-a)²=0 ???? Mr humber | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 17:36 Sam 23 Fév 2013, 17:36 | |
| - k.abdo a écrit:
- comment tu trouve l'éqoition :
(a-2b)²+(b-3c)²+(3c-a)²=0 ???? Mr humber a²+4b²+9b²=2ab+3bc+6ac | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Sam 23 Fév 2013, 18:16 Sam 23 Fév 2013, 18:16 | |
| - Humber a écrit:
- nmo a écrit:
- nmo a écrit:
- Exercice4: (BLR MC)
Soit 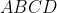 un quadrilatère inscriptible (inscrit dans un cercle) tel que un quadrilatère inscriptible (inscrit dans un cercle) tel que 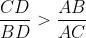 . .
Montrer que 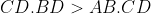 . . Soit 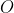 l'intersection des deux diagonales de ce quadrilatère. l'intersection des deux diagonales de ce quadrilatère.
On a 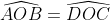 et et 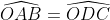 . .
Donc les deux triangles 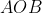 et et 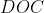 sont semblables, d'où: sont semblables, d'où: 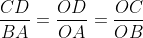 .==>(*) .==>(*)
On pose désormais: 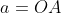 , , 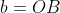 , , 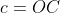 et et 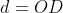 . .
L'inégalité à démontrer s'écrit: 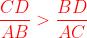 , ou encore , ou encore 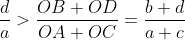 selon *. selon *.
Soit 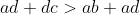 , ou encore , ou encore 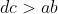 .==>(**) .==>(**)
D'un autre coté, on a  , soit , soit 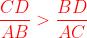 . .
Avec les notation introduite, ça devient 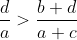 , en utilisant encore *. , en utilisant encore *.
Ce qui donne: 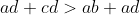 , ou bien , ou bien 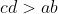 . .
Ce qui achève la démonstration.
Sauf erreurs! L"équivalence que vous avez faites est fausse à ce que je vois, pourriez vous réviser ce qui est en rouge ? J'ai corrigé ma réponse! C'était une faute d'inattention... | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 | |
  | |
k.abdo
Féru

 Nombre de messages : 32 Nombre de messages : 32
Age : 28
Date d'inscription : 14/04/2012
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  Dim 24 Fév 2013, 01:44 Dim 24 Fév 2013, 01:44 | |
| ok c'est ça bien ..  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiade de première, deuxième étape, premier test: Sujet: Re: Olympiade de première, deuxième étape, premier test:  | |
| |
|
  | |
| | Olympiade de première, deuxième étape, premier test: |  |
|
