| | Exercices d'olympiades: |  |
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Exercices d'olympiades: Sujet: Exercices d'olympiades:  Dim 07 Fév 2010, 11:33 Dim 07 Fév 2010, 11:33 | |
| 1/ABCD est un parallélogramme.
E et F sont deux points du plan tel que: AE=(2/3)AB et BF=(-1/2)BC.(vecteurs).
Montrez que les points D, E, et F son allignés.
2/Soit (E) l'équation suivante:
xV(12+8/7)-V(192+128/7)=0.
Montrez que la solution de l'équation (E) est rationnelle.
3/ABC est un triangle et (C) son cercle surconscrit.
Le bissectrice de l'angle BAC coupe (BC) en E et le cercle (C) en F.
Montrez que (BF) est tangente du cercle C' circonscrit au triangle ABE.
P.S: Ce sont des exercices de l'année précédante dans la phase éléminatoire des olympiades.
Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Dim 07 Fév 2010, 12:51 Dim 07 Fév 2010, 12:51 | |
| Le troisième est le plus intéressant.  %20\text{%20tangente%20\%60a%20}%20(C%27)%20&\Leftrightarrow%20\widehat{ABF}%20=%20180%20-%20\widehat{AEB}%20\\%20&\Leftrightarrow%20\widehat{ABF}%20=%20\widehat{BAE}%20+%20\widehat{ABE}%20\\%20&\Leftrightarrow%20\widehat{EBF}%20=%20\widehat{BAE}%20\\%20&\Leftrightarrow%20\widehat{EBF}%20=%20\widehat{EAC}%20\\%20\end{align*}) Qui est vraie d'après le théorème de l'angle inscrit. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Dim 07 Fév 2010, 13:17 Dim 07 Fév 2010, 13:17 | |
| Les élèves du collège n'ont pas encore étudier ce genre de démonstration.
Il y a deux autres méthodes pour résoudre cet exercice et qui sont du niveau collège.
Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Dim 07 Fév 2010, 14:08 Dim 07 Fév 2010, 14:08 | |
| - nmo a écrit:
- Les élèves du collège n'ont pas encore étudier ce genre de démonstration.
Je ne vois pas ce qu'il y a d'"ésotérique" dedans ? Ma démonstration ne fait intervenir que le théorème de l'angle inscrit... | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Lun 08 Fév 2010, 18:58 Lun 08 Fév 2010, 18:58 | |
| Ce que je veut dire que les collégiens commencent par toujours par les données et arrivent au résultat.
Toi, tu as fait le contraire. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Sam 13 Fév 2010, 18:53 Sam 13 Fév 2010, 18:53 | |
| 4/Montrez que 1/(n+V2)<1/V2 pour tout n naturel non nul.
En déduire que:1/(1+V2)+1/(2+V2)+1/(3+V2)+...+1/(9+V2)<5V2.
5/Dans le plan muni d'un repère cartésien orthogonal orthonormé (O,I,J), on considère les points E(-3,1), F(0,1), G(3,-2), et H(-6,-2).
* Ecrivez HG en fonction de EF. (vecteurs).
*Comparez EH et FG.
*En déduire la nature du quadrilatère EFGH avec justification.
P.S: c'est la suite et fin des exercices.
Bonne chance.
Dernière édition par nmo le Ven 05 Mar 2010, 15:21, édité 1 fois | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 13:17 Ven 05 Mar 2010, 13:17 | |
| tu peux poster la solution du premier exercice j ariive pas à le resooudre | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 15:23 Ven 05 Mar 2010, 15:23 | |
| - Azerty1995 a écrit:
- tu peux poster la solution du premier exercice j ariive pas à le resooudre
Je vais répondre sur tout le test. Attends mes prochains messages. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 15:35 Ven 05 Mar 2010, 15:35 | |
| Pour le deuxième: On a 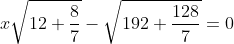 . Donc 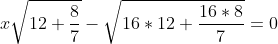 . Donc }=0) . Donc 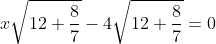 . Donc  \sqrt{12+\frac{8}{7}}=0) . Et puisque V(12+8/7)#0. Il s'ensuit que 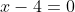 . Donc 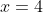 . Donc la solution de l'équation (E) est rationnelle.
Dernière édition par nmo le Ven 05 Mar 2010, 15:44, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 15:43 Ven 05 Mar 2010, 15:43 | |
| Pour le premier:
Première methode: (vecteur dans tout qui suit)
On a DE=DA+AE.
Donc DE=AE-AD.
Donc DE=(2/3)AB-AD.==>(1)
Et on a DF=DA+AB+BF.
Donc DF=-AD+AB-(1/2)BC.
Donc DF=-AD-(1/2)AD+AB.
Donc DF=-(3/2)AD+AB.==>(2)
Et de 1 et 2, on a -3/2DE=DF.
Donc les points D, E, et F sont allignés. | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 15:44 Ven 05 Mar 2010, 15:44 | |
| Bien joué^^ merci pour ta solution | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 15:52 Ven 05 Mar 2010, 15:52 | |
| Pour le premier:
Deuxième methode: (vecteur dans tout qui suit)
On a AE=(2/3)AB et BF=-(1/2)BC.
Donc 3AE=2AB et -BC=2BF.
Donc 3AE=2AB et -AD=2BF.
Donc 3AE-AD=2AB+2BF.
Donc 3AE-AD=2AF.
Donc 3AE=AD+2AF.
Donc 3AE=AE+ED+2AE+2EF.
Donc 3AE=3AE+ED+2EF.
Donc 0=ED+2EF.
Donc ED=-2EF.
Donc les points D, E, et F sont allignés. | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 16:02 Ven 05 Mar 2010, 16:02 | |
| j'ai trouvé une deuxième méthode:(tout est en vecteurs)
On sait que AE=(2/3)AB alors EB=(1/3)AB
On a :
EF=EB+BF
EF=(1/3)AB-(1/2)BC
DE=DA+AE
DE=(2/3)AB-BC
DE=2((1/3)AB-(1/2)BC)
DE=2EF
Alors les points D,E,F sont allignés. | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 16:03 Ven 05 Mar 2010, 16:03 | |
| | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 16:03 Ven 05 Mar 2010, 16:03 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 16:09 Ven 05 Mar 2010, 16:09 | |
| Pour le quatrième: 1/On a n un entier naturel. Donc 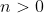 . Donc 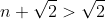 . Donc 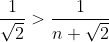 . 2/On remplace n par 1 et 2 et 3 et ... et 10. On obtient 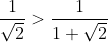 et 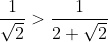 et 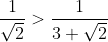 et ... et 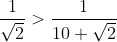 . Donc  . Et on a 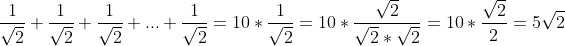 . Donc  . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 16:11 Ven 05 Mar 2010, 16:11 | |
| - Azerty1995 a écrit:
- j'ai trouvé une deuxième méthode:(tout est en vecteurs)
On sait que AE=(2/3)AB alors EB=(1/3)AB
On a :
EF=EB+BF
EF=(1/3)AB-(1/2)BC
DE=DA+AE
DE=(2/3)AB-BC
DE=2((1/3)AB-(1/2)BC)
DE=2EF
Alors les points D,E,F sont allignés. C'est ma deuxième méthode pour résoudre l'exercice et elle est juste. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 16:33 Ven 05 Mar 2010, 16:33 | |
| Pour le cinquième: On a ) . Donc ) . Donc ) .==>(1) Et on a ) . Donc ) . Donc ) .==>(2) Et de 1 et 2 on déduit que 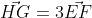 . 2/On a ^2+(y_G-y_F)^2}=\sqrt{(3-0)^2+(-2-1)^2}=\sqrt{(3)^2+(-3)^2}=\sqrt{9+9}=\sqrt{18}) . Et on a ^2+(y_H-y_E)^2}=\sqrt{(-6+3)^2+(-2-1)^2}=\sqrt{(-3)^2+(-3)^2}=\sqrt{9+9}=\sqrt{18}) . Donc 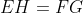 . 3/De la première et la deuxième question, on déduit que le quadrilatère EFGH est un trapèze isocèle sa petite base est [EF] et sa grande base est [HG]. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 16:54 Ven 05 Mar 2010, 16:54 | |
| Pour le troisième:
Première méthode:
On a O' le centre du cercle (C').
Posons EAC=EAB=a et O'BE=b. (angles)
On a CAF=EBF car ce sont deux angles inscrits dans le cercle (C) limitant le même arc [CF].
Et on a BO'E=2BAE (angles) car ce sont deux angles associés au centre périphériques.
Donc BO'E=2a. (angle)
D'autre part, on a O'BE est un triangle isocèle en O' car O'E et O'B sont deux rayons du cercle (C')
Donc O'BE=O'EB=b. (angles)
Dans le triangle BO'E+BEO'+O'BE=180°. (angles)
Donc 2a+b+b=180°.
Donc 2a+2b=180°.
Donc 2(a+b)=2*90°.
Donc a+b=90°.
Et on a O'BF=O'BE+EBF. (angles)
Donc O'BF=b+a. (angle)
Donc O'BF=90°. (angle)
Il s'ensuit que (BF) et (O'B) sont perpendiculaires.
C'est à dire que (BF) tangente à (C'). | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 18:14 Ven 05 Mar 2010, 18:14 | |
| Pour le troisième:
Deuxième méthode:
On a O' le centre du cercle (C') et [BG] diamètre dans le même cercle.
On a BAG=90° (angle) car c'est un angle inscrit limitant un demi-cercle.
Donc AGB+GBA=90° (angles) car ce sont deux angles supplémentaires dans le triangle AGB.
Donc AGE+EGB+GBA+90°.==>(1) (angles)
Et on a ABE=AGE (angles) car ce sont deux angles inscrits dans le cercle (C') limitant le même arc [AE].==>(2)
Et on a BGE=BAE (angles) car ce sont deux angles inscrits limitant le même arc [BE].
Et on a FBC=FAC (angles) car ce sont deux angles inscrits limitant le même arc [FC].
Et on a [AE) est bissectrice de l'angle BAC.
Donc EAB=FAC. (angles)
Donc BGE=FBC.==>(3) (angles)
Ainsi la relation 1 peut s'écrire en utilisant 2 et 3 comme suit: ABE+FBC+GBA=90°. (angles)
Donc GBF=90°. (angle)
Il s'ensuit que (BF) et (O'B) sont perpendiculaires.
C'est à dire que (BF) tangente à (C'). | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  Ven 05 Mar 2010, 18:16 Ven 05 Mar 2010, 18:16 | |
| Pour l'information, les premières méthodes sont du professeur et les deuxièmes sont les miennes. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Exercices d'olympiades: Sujet: Re: Exercices d'olympiades:  | |
| |
|
  | |
| | Exercices d'olympiades: |  |
|
