| | Montrer une inégalité. |  |
|
+4Thalès the kiler reda-t Calculus 8 participants |
| Auteur | Message |
|---|
Calculus
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 30
Date d'inscription : 26/02/2010
 |  Sujet: Montrer une inégalité. Sujet: Montrer une inégalité.  Ven 26 Fév 2010, 20:13 Ven 26 Fév 2010, 20:13 | |
| Soit a, b et c des réels positifs.
Montrer que : a^3+b^3+c^3>=3abc. | |
|
  | |
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Ven 26 Fév 2010, 20:34 Ven 26 Fév 2010, 20:34 | |
| très facile ¨^^
<==> 1/2(a+b+c)((a-b)²+(b-c)²+(a-c)²) >=0 | |
|
  | |
Calculus
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 30
Date d'inscription : 26/02/2010
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Ven 26 Fév 2010, 20:42 Ven 26 Fév 2010, 20:42 | |
| Merci.
Je peux savoir, s'il te plaît, quelle inégalité, (forme générale) on utilise dans ce genre d'exercices ? | |
|
  | |
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Ven 26 Fév 2010, 21:00 Ven 26 Fév 2010, 21:00 | |
| non là je n'ai pas utilisé une inégalité spéciale: l'inégalité que tu nous a proposé s'écrit comme cela X^3+Y^3+Z^3 - 3XYZ=1/2(a+b+c)((a-b)²+(b-c)²+(a-c)²) qui est >= 0 donc l'inégalité est juste! | |
|
  | |
the kiler
Maître
 Nombre de messages : 192 Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Ven 26 Fév 2010, 21:04 Ven 26 Fév 2010, 21:04 | |
| voici la forme general: I.A.G (inegalités entre la moyenne arithmetique et geometrique)  | |
|
  | |
Calculus
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 30
Date d'inscription : 26/02/2010
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Ven 26 Fév 2010, 21:37 Ven 26 Fév 2010, 21:37 | |
| Merci à tous les deux.
La première méthode n'est pas facile à deviner et, si l'on veut développer le tout (ou factoriser, dans l'autre sens) pour faire une démonstration convaincante, il nous faudra plusieurs lignes (sans sauter d'étapes). Par contre, elle n'est pas du tout hors programme !
La deuxième tient en une ligne mais, est-il permis d'utiliser des inégalités et autres théorèmes hors programme ? | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 11:47 Sam 27 Fév 2010, 11:47 | |
| Aux Olympiades, on peux utiliser ce genre d'inégalités comme I.A.G, Cauchy-Schwartz, Chebychev etc...même s'ils sont tous hors programme.
Par contre si tu as ce genre d'inégalités à prouver dans un DS à l'école, il faudra bricoler avec les trucs standards de collège pour les prouver. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 19:02 Sam 27 Fév 2010, 19:02 | |
| Voici une autre inégalité se basant sur la tienne:
Démontrer que pour chaque a,b,c>0
(a+b+c)^3 >= 27abc.
Bonne chance. | |
|
  | |
Math=life
Maître
 Nombre de messages : 105 Nombre de messages : 105
Age : 33
Date d'inscription : 12/02/2010
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 19:10 Sam 27 Fév 2010, 19:10 | |
| Par I.A.G on a:
(a+b+c)/3>=(abc)^(1/3)
don puisque les deux parties de cette inégalité sont positives, on peut tout elever au cube , donc:
[(a+b+c)/3]>=[(abc)^1/3]^3=abc
soit: [(a+b+c)^3]/27>=abc
donc en multipliant par 27 on obtient:
(a+b+c)^3>=27abc
CQFD | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 19:33 Sam 27 Fév 2010, 19:33 | |
| Il existe deux autres solutions sans utilisation des théorèmes.
Pour ta solution, je ne peux pas juger car je ne sais pas comment appliquer I.A.G, peux-tu m'éclairer. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 19:37 Sam 27 Fév 2010, 19:37 | |
| Une autre question:
En utilisant : a^3+b^3+c^3>=3abc.
Montrez que (a^2+1)/b + (b^2+1)/c + (c^2+1)/a >=6.
Bonne chance. | |
|
  | |
Math=life
Maître
 Nombre de messages : 105 Nombre de messages : 105
Age : 33
Date d'inscription : 12/02/2010
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 19:43 Sam 27 Fév 2010, 19:43 | |
| si vous ne connaissez pas I.A.G renseignez vous en  | |
|
  | |
Calculus
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 30
Date d'inscription : 26/02/2010
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 20:54 Sam 27 Fév 2010, 20:54 | |
| - nmo a écrit:
- Voici une autre inégalité se basant sur la tienne:
Démontrer que pour chaque a,b,c>0
(a+b+c)^3 >= 27abc.
Bonne chance. En se basant sur la mienne, comme tu dis : On a la mienne : A^3+B^3+C^3>=3ABC On pose : a=A^3, b=B^3 et c=C^3 Donc : a+b+c>=3 RACINECUBIQUE(abc) a, b et c sont positifs (on le sait déjà) On lève au carré et c'est CQFD | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 22:49 Sam 27 Fév 2010, 22:49 | |
| - nmo a écrit:
- Une autre question:
En utilisant : a^3+b^3+c^3>=3abc.
Montrez que (a^2+1)/b + (b^2+1)/c + (c^2+1)/a >=6.
Bonne chance. (a^2+1)/b + (b^2+1)/c + (c^2+1)/a >=2a/b +2b/c +2c/a >=2(a/b+b/c+c/a) >= 2.3=6 (a^3+b^3+c^3>=3abc..) | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 23:18 Sam 27 Fév 2010, 23:18 | |
| Les questions que vous êtes entrain d'avancer sont des applications directs d'I.A.G, je vous conseille de comprendre le principe et de l'appliquer ensuite dans la résolution d'inégalités
En utilisant I.A.G, je peux vous proposer de démontrer :
(x+y+z)(xy+yz+zx)>=9xyz (tel que x;y;z>0)
Déjà c'est facile de le démontrer puisque c'est aussi du Cauchy-Schwartz :
<=> (x+y+z).xyz(1/x+1/y+1/z)>=9xyz
<=> (x+y+z)(1/x+1/y+1/z)>=9 (xyz>0) | |
|
  | |
Calculus
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 30
Date d'inscription : 26/02/2010
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 23:41 Sam 27 Fév 2010, 23:41 | |
| @Thalès :
Pourrais-tu nous faire un petit cours sur ces deux inégalités particulièrement efficaces, s'il te plaît ? | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Sam 27 Fév 2010, 23:50 Sam 27 Fév 2010, 23:50 | |
| Bon déjà pour I.A.G le principe est assez simple :
(x1+x2+...+xn)>= n . rac nième de (x1.x2....xn)
ce qui donne pour n=3 par exemple :
a+b+c>= 3 racine cubique de abc, et si tu élève au cube ça te donne : (a+b+c)^3>=27abc (c'est ce que vous avez déjà vu)
Pour l'inégalité que j'ai proposé c'est le même principe, tu as aussi :
ab+bc+ca>3 rac cubique de (a²b²c²) (car ab.bc.ca=a²b²c²)
et puisque a+b+c>=3 rac cubique de (abc)
Si tu fais le produit de ces deux inégalités :
(ab+bc+ca)(a+b+c)>9 rac cubique de a^3b^3c^3 = 9abc
Et pour cauchy schwartz c'est aussi simple il suffit de voir la relation pour bien la saisir. | |
|
  | |
Calculus
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 30
Date d'inscription : 26/02/2010
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Dim 28 Fév 2010, 12:33 Dim 28 Fév 2010, 12:33 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Dim 28 Fév 2010, 17:33 Dim 28 Fév 2010, 17:33 | |
| Voici la première méthode:
Remarquons que: (a+b+c)^3= a^3+b^3+c^3+ 3( a²b+a²c+b²c+ab²+ac²+bc²)+6abc (*)
Sachant que pour chaque réels x et y x^2+y^2>=2xy.
Donc:
a²b+bc²>=2rac(a²b)*rac(bc²)= 2abc.
a²c+b²c>=2rac(a²c)*rac(b²c)= 2abc.
ab²+ac²>=2rac(ab²)*rac(ac²)= 2abc.
Alors 3(a²b+a²c+b²c+ab²+ac²+bc²)>= 18 abc.
Donc 3(a²b+a²c+b²c+ab²+ac²+bc²)+6abc>= 24abc (**)
Et on a a^3+b^3+c^3>= 3abc (***)
En déduisant de (*) et (**) et (***)
On trouve a^3+b^3+c^3+3(a²b+a²c+b²c+ab²+ac²+bc²)+6abc >= 27abc.
Soit en résumé: (a+b+c)^3>= 27abc. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Dim 28 Fév 2010, 17:41 Dim 28 Fév 2010, 17:41 | |
| Voici la deuxième méthode:
On a: (a+b+c)²>=3(ab+ac+bc)
Donc (a+b+c)^3>=3(a+b+c)(ab+bc+ac).==>(1)
Après le développement on procède comme ça:
a²+b²>=2ab.
a²c+b²c>=2abc.
Donc (a+b+c)(ab+ac+bc)>=9abc. (Déja annoncé par Thalès)
Donc 3(a+b+c)(ab+ac+bc)>=27abc.==>(2)
Et de 1 et 2 on déduit le résultat:(a+b+c)^3>=27abc. | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Lun 01 Mar 2010, 13:15 Lun 01 Mar 2010, 13:15 | |
| Il faut savoir que Am Gm est une inégalité très puissante même si elle paraît simple, et résoud beaucoup de problèmes, faut bien la maîtriser et l'appliquer. | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 | |
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Mar 02 Mar 2010, 16:02 Mar 02 Mar 2010, 16:02 | |
| - Sylphaen a écrit:
- nmo a écrit:
- Une autre question:
En utilisant : a^3+b^3+c^3>=3abc.
Montrez que (a^2+1)/b + (b^2+1)/c + (c^2+1)/a >=6.
Bonne chance. (a^2+1)/b + (b^2+1)/c + (c^2+1)/a >=2a/b +2b/c +2c/a
>=2(a/b+b/c+c/a)
>= 2.3=6 (a^3+b^3+c^3>=3abc..) Tu n'as pas utilisé a^3+b^3+c^3>=3abc. Car 2a/b+2b/c+2c/a=>6. Donne a/b+b/c+c/a=>3. Ce qui est équivalent à ca^2+ab^2+cb^2>=3abc et pas à a^3+b^3+c^3>=3abc. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  Mar 02 Mar 2010, 18:44 Mar 02 Mar 2010, 18:44 | |
| Si si , c'est la même chose .. : 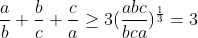 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Montrer une inégalité. Sujet: Re: Montrer une inégalité.  | |
| |
|
  | |
| | Montrer une inégalité. |  |
|
