| | Inégalité (Own) |  |
|
|
| Auteur | Message |
|---|
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Inégalité (Own) Sujet: Inégalité (Own)  Dim 07 Mar 2010, 11:52 Dim 07 Mar 2010, 11:52 | |
|
Dernière édition par MohE le Dim 07 Mar 2010, 13:14, édité 1 fois | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Dim 07 Mar 2010, 12:48 Dim 07 Mar 2010, 12:48 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Dim 07 Mar 2010, 13:06 Dim 07 Mar 2010, 13:06 | |
| 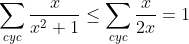 . ^2}{(1+xy)^2}%20=%20\frac{(1+1)(1+(xy)^2)}{(xy+1)^2}%20\geq%20\frac{(1+xy)^2}{(xy+1)^2}%20=%201) . (  ) D'où : ^2}{(1+xy)^2}) . PS : Pour que la syntaxe soit correcte, il faudrait penser à ajouter la condition : 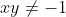 . | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Dim 07 Mar 2010, 13:11 Dim 07 Mar 2010, 13:11 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Dim 07 Mar 2010, 13:20 Dim 07 Mar 2010, 13:20 | |
| Ta remarque est pertinente, merci. Je corrige donc la première ligne : Il est connu que : 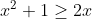 , pour tout réel x. D'où : 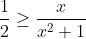 ( 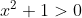 ) En sommant, il vient que : 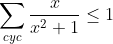 . | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Dim 07 Mar 2010, 15:15 Dim 07 Mar 2010, 15:15 | |
| Personne?!! essayait encore, c'est vraie que c'est un peu difficile mais ce n'est pas impossible. | |
|
  | |
hammadioss
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 30
Localisation : fes
Date d'inscription : 30/09/2008
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Mar 09 Mar 2010, 14:29 Mar 09 Mar 2010, 14:29 | |
| elle n'est pas très difficile ta (own) à démontrer mais je crois qu'elle pourrais être utile (en tout cas elle me semble un peu familier :/)
soit x et y deux réels:
on a (1+x²)(y²+1)>=x(1+y²)+y(1+x²) ------- (d'après un test d'olympiade de cette année si vous en souvenez ^^)
<=> [x(1+y²)+y(1+x²)]/[(1+x²)(y²+1)]=<1
alors que : 1+(1-xy)²/(1+xy)² >= 1
donc : 1 + (1-xy)²/(1+xy)² >= x/(x²+1) + y(y²+1)
CQFD
ps: ça me prend un peu du temps pour écrire en latex alors desolé pour la mal écriture | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 | |
  | |
codex00
Expert sup

 Nombre de messages : 2122 Nombre de messages : 2122
Age : 34
Localisation : No where !!!
Date d'inscription : 30/12/2006
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Dim 28 Mar 2010, 16:23 Dim 28 Mar 2010, 16:23 | |
| C'est moche comme solution mais c'est une solution  IAG => x²+3>= 4x^(1/2) alors il suffit de montrer que: lxl^1/2 +lyl^1/2 + 4xy/(1+3x²y²) =< 3 en considérant f(x,y)=lxl^1/2 +lyl^1/2 + 4xy/(1+3x²y²) et en calculant df/dx et df/dy df/dx=df/dy=0 => x²y²=1/3 ou x=y en traitant chacun des cas on trouve que f admet un maximum local pour tout point vérifiant xy=1/(3^1/2) et un minimum local pour xy=-1/(3^1/2) donc pour n'importe quel réels (x1,y1) vérifiant p1=x1y1=1/(3^1/2) on a f(x,y)=<f(x1,y1) = 2,914536224 =< 3  | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Dim 28 Mar 2010, 18:19 Dim 28 Mar 2010, 18:19 | |
| - codex00 a écrit:
- C'est moche comme solution mais c'est une solution
IAG => x²+3>= 4x^(1/2)
alors il suffit de montrer que:
lxl^1/2 +lyl^1/2 + 4xy/(1+3x²y²) =< 3
en considérant f(x,y)=lxl^1/2 +lyl^1/2 + 4xy/(1+3x²y²)
et en calculant df/dx et df/dy
df/dx=df/dy=0 => x²y²=1/3 ou x=y
en traitant chacun des cas on trouve que f admet un maximum local pour tout point vérifiant xy=1/(3^1/2) et un minimum local pour xy=-1/(3^1/2)
donc pour n'importe quel réels (x1,y1) vérifiant p1=x1y1=1/(3^1/2)
on a f(x,y)=<f(x1,y1) = 2,914536224 =< 3
Bonsoir codex00! mon niveau modeste ne me permet pas de comprendre cette solution, cependant, j'ai quelques remarques: rouge=> Là, tu as ignoré le cas ou x ou y sont négatifs.vert=> Ici, ca doit être strictement inferieur<.Aussi il y a quelques choses qui renforce mon doute a propos de la verité de ta solution, pour ce qui est en mauve, pourquoi la fonction doit-elle avoir un minimum, surtout en xy=1/3, puisqu'on voit clairement que cette fontion prend toujours une valeur minimal lorsque x et y tendent vers 0. encore la dernière ligne prouve que l'inegalité est stricte, Or, on peux remarqué qu'il y a un cas d'égalité, c'est lorsque x=y=1, il y a surement quelques choses qui clochent dans ta solution, surtout que j'arrive pas à comprendre le methode tout entiere.
P.S: je serai très content, si tu m'explique ta solution en detaille, soit par poste, soit par mp, merci en tout cas. | |
|
  | |
codex00
Expert sup

 Nombre de messages : 2122 Nombre de messages : 2122
Age : 34
Localisation : No where !!!
Date d'inscription : 30/12/2006
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Dim 28 Mar 2010, 23:42 Dim 28 Mar 2010, 23:42 | |
| voilà  | |
|
  | |
imanos
Féru

 Nombre de messages : 66 Nombre de messages : 66
Age : 30
Date d'inscription : 09/02/2010
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  Lun 29 Mar 2010, 17:30 Lun 29 Mar 2010, 17:30 | |
| Bonjour voici ton inego est ekivalente a:  si x =<0 ou y=<0 l'inégalitée est bien équivalente on travaille mnt qu'avec x>0 et y>0 on pose z=1/p on aura xyz=1 donc linego est ékivalente a :  éqyuvakente a : (y^{2}+3)(z^{2}+3)=\sum&space;28+3(x^{2}z^{2}+y^{2}x^{2}+y^{2}z^{2})+9(x^{2}+y^{2}+z^{2})-4yz-12x(y^{2}+z^{2})-36x=84+9(x^{2}z^{2}+z^{2}y^{2}+x^{2}y^{2})+27(x^{2}+y^{2}+z^{2})-12xy(x+y)-12yz(y+z)-12xz(x+z)-36(x+y+z)-4(xy+xz+yz)) et on sait que: x²y²+x²z²+y²z²=(xy+xz+yz)²-2(x+y+z) et x²+y²+z²=(x+y+z)²-2(xy+yz+yz) et puisque 84=120-12xyz-12xyz-12xyz on pose x+y+z=a et xy+yz+xz=b donc on aura A=9b²+27a²-12ab-58b-54a+120 A=9(a-3)²+6(a-b)²+3(b-3)²+12a²-40b+12 donc il suffit de montrer que 12a²-40b+12>=0 <==>3a²+3>=10b <==> 3(x+y+z)²+3>=10(xy+xz+yz) <==> 3(x²+y²+z²)+3>=4(xy+xz+yz) or on a 2(x²+y²+z²)>=2(xy+xz+yz) donc il suffit de montrer que x²+y²+z²+3>=2(xy+xz+yz) <==> x²+y²+z²+2xyz+1>=2(xy+xz+yz) ce qui n'est pas difficile a démontrer A+ | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Inégalité (Own) Sujet: Re: Inégalité (Own)  | |
| |
|
  | |
| | Inégalité (Own) |  |
|
